Реферат: Многопозиционная фазовая модуляция в системах спутниковой связи с МДЧ

p/2

\/2*E=1.41*\/E

3.01

3

8

p/4

\/(2-\/2)E=0.765\/E

8.34

4

16

p/8

\/(2--\/2+\/2)E=

=0.39\/E

14.2

5

32

p/16

\/(2--\/2+\/2+\/2)E=

=0.196\/E

20.2

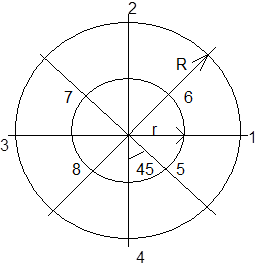
Равномерное размещение всех сигнальных точек на окружности, т.е. использование равномощных сигналов, отличающихся лишь фазой, является оптимальным только для 2-х, 3-х и 4-х позиционных случаев. При m>4 оптимальными будут неравномощные сигналы, которые кроме отличия по фазе имеют различие по амплитуде. Размещены они равномерно, обычно внутри окружности, радиус которой определяется максимально допустимой энергией сигнала. С точки зрения теории модуляции такие сигналы относятся к сигналам с комбинированной модуляцией, при которой одновременнo изменяется несколько параметров сигнала. В данном случае амплитуда и фаза (сигналы с амплитудно-фазовой манипуляцией АФМн). Простейший принцип построения сигналов с АФМн состоит в том, что сигнальные точки размещаются на двух концентрических окружностях. Однако, этот путь не всегда приводит к оптимальному результату. Например: 8-ми позиционный сигнал с АФМн:

___

4 сигнала размещены на окружности с радиусом R=\/E , а 4 на окружности r<R со сдвигом по фазе p/4 (сигнальные точки расположены рядом с их соответствующими номерами). Данная совокупность сигналов оптимизируется по критерию максимума минимального расстояния между сигналами, путём выбора отношения радиусов R и r. Оптимальное отношение R/r=1.932 определяется чисто из геометрических соображений: чем больше r, тем больше расстояние между сигнальными точками окружности радиуса r, но тем меньше расстояния между этими точками и токами окружности радиуса R. Пэтому искомый максимум R/r достигается тогда, когда эти расстояния будут равны т.е. равносторонним будет треугольник 854, а это будет только тогда, когда искомое отношение равно указанному. При этом оптимальном отношении минимальное расстояние между сигналами d8=0.73\/E (см.7.стр.51). Это расстояние меньше,чем у системы 8-ми позиционных ФМн-сигналов, расположенных на одной окружности радиуса R(см. последнюю таблицу). Таким образом, в случае трехкратной системы размещение сигнальных векторов на двух концентрических окружностях не дает выигрыша. Оптимальным по критерию максимума минимального расстояния оказывается простейшая 8-ми позиционная система с АФМн, у которой 7 сигнальных точек размещены на окружности радиуса R=\/E, а восьмой сигнал равен нулю:

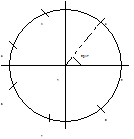
МИНИМАЛЬНОЕ РАССТОЯНИЕ У ТАКОЙ СИСТЕМЫ d8=0.86\/E, ЧТО БОЛЬШЕ, ЧЕМ d8 ФМн.

Далее рассмотрим 16-позиционные АФМн-сигналы.

Расстояние между ближайшими сигнальными точками в 16-ти позиционной ФМн системе d16=0.39\/E, что соответствует проигрышу в 14.2 дБ по сравнению с 2-х позиционной (см. посл. табл.). В круге данного радиуса можно построить лучшую систему сигналов с АФМн. Примером построения такой системы является система, у которой нечётные сигналы равномерно размещены на окружности большого радиуса с интервалом p/4, а чётные -- с тем же интервалом на окружности меньшего радиуса, но с общим сдвигом по фазе относительно нечётных на угол p/8: