Реферат: Множественная регрессия
3. Следует избегать дублирования факторов. Каждый реальный фактор должен быть представлен одним показателем. Например, трудовой фактор в модели объема продукции может быть представлен либо среднесписочным числом работников, либо затратами человеко-дней (человеко-часов) на производство продукции, но не обоими показателями. Дублирование факторов ведет к раздроблению влияния фактора, и он может оказаться ненадежным из-за такого раздробления.
4. Следует по возможности избегать факторов, тесно связанных с другими.
5. Следует включать факторы одного уровня иерархии, не следует включать и факторы вышележащего уровня и их субфакторы. Например, в модель себестоимости зерна включаем урожайность, трудоемкость, но не добавляем еще балл плодородия, дозу удобрений, энерговооруженность работников, т.е. субфакторы – причины, влияющие на урожайность и трудоемкость. Включение субфакторов тоже дублирование фактора.
6. Есть логика в таком построении модели, при котором все признаки отнесены на одну и ту же единицу совокупности, как результативный признак, так и факторы. Например, если моделируется объем продукции предприятия, то и факторы должны относиться к предприятию: число работников, площадь угодий, основные фонды и т.д. Если строится модель заработной платы работника, то и факторы должны относиться к работнику: его стаж, возраст, образование, разряд тарифной сетки (шкалы), энерговооруженность и т.д.
7. Действует принцип простоты модели. Если возможно построить хорошую модель с пятью факторами, то не следует гнаться за идеальной моделью с десятью факторами, обычно лишние факторы ухудшают модель.
4. Системы показателей многофакторной корреляции и регрессии
Рассмотрим данную систему показателей на примере связи урожайности зерновых культур в 51 агрофирме Орловской области. Первоначально были отобраны 8 факторных признаков, которые могут влиять на вариацию урожайности:
x 1 – размер посевной площади зерновых, га;
x 2 – удельный вес зерновых в общей площади, %;
x 3 – затраты на 1 га посева зерновых, тыс. руб./га;
x 4 – затраты труда на 1 га, чел.-ч;.
x 5 – уровень оплаты труда, руб./чел.-ч.;
x 6 – энергообеспеченность, л.с./100 га пашни;
x 7 – число комбайнов на 1000 га зерновых, шт.;
x 8 – число трактористов-машинистов на 100 га пашни, чел.
Первоначальное уравнение регрессии имеет вид:
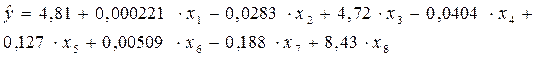
Однако надежно отличными от нуля оказались только коэффициенты при x 3 (t -критерий равен 10,5) и при x 8 (t -критерий равен 2,72). Большую надежность, чем другие факторы имеет и x 5 .
После отсева ненадежных факторов, т.е. исключения их из уравнения, окончательное уравнение регрессии таково:
![]()
Таким образом, на различие урожайности в данных 51 агрофирмы сильнее всего и надежно повлияли различия между предприятиями в затратах на 1 га, в уровне оплаты труда и в обеспеченности квалифицированными работниками.
Каждый из коэффициентов, называемых коэффициентами чистой регрессии, интерпретируются как величина изменения урожайности при условии, что данный фактор изменяется на принятую единицу измерения, а два других фактора остаются постоянными на средних уровнях. Например, b 3 означает, что при увеличении затрат на 1 га зерновых и при неизменности оплаты труда и обеспеченности трактористами-машинистами урожайность в среднем увеличивалась в среднем на 4, 6 ц/га. Термин «условно чистая регрессия» означает, что влияние отдельного фактора очищено от сопутствующей вариации только тех факторов, которые входят в уравнение, но не очищено от возможной сопутствующей вариации других факторов.
Величина коэффициентов условно чистой регрессии зависит от принятых единиц измерения. Если бы фактор x 3 измерялся не в тысячах рублей на гектар, а в рублях на гектар, то коэффициент b 3 был бы равен 0,00461 руб./га. Следовательно, сравнивать между собой коэффициенты условно чистой регрессии нельзя. Чтобы получить сравнимые коэффициенты влияния вариации факторов на вариацию результата, следует избавиться от единиц измерения, привести к одной условной единице. Для этого можно применить два способа.
Первый способ называется стандартизацией. Этот термин возник из английского названия среднего квадратического отклонения (Standarddeviation). Стандартизированные коэффициенты регрессии выражаются в долях или величинах, если они превышают единицу – в величинах σy . Стандартизированные коэффициенты обозначают греческой буквой β и называют бета-коэффициентами. Их формула такая:
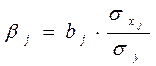 (24)
(24)
В нашем примере получаем:
β 3 = 0,772;
β 5 = 0,147;
β 8 = 0,223.
Интерпретация бета-коэффициентов такова: при изменении фактора x 3 на одно его среднее квадратическое отклонение от средней величины и при постоянстве других факторов результативный признак (урожайность) отклонится от своего среднего уровня на 0,772 его среднего квадратического отклонения. Так как все стандартизированные коэффициенты выражены в одинаковых единицах измерения, в σy , они сравнимы между собой, и можно сделать вывод, что на вариацию урожайности сильнее всего повлияла в изучаемой совокупности предприятий вариация затрат на гектар посева.
Другой способ приведения коэффициентов регрессии к сравнимому виду – их преобразование в коэффициенты эластичности. Формула коэффициента эластичности ℓj :