Реферат: Множественная регрессия

Интерпретируется коэффициент эластичности следующим образом: при изменении фактора x_j на его среднюю величину и при постоянстве других входящих в уравнение факторов результативный признак в среднем изменится на ℓ_j части его средней величины (или на ℓ_j средних, если ℓ_j >1, что бывает реже). Часто говорят, «изменится на ℓ_j процентов на 1% изменения фактора».

В нашем примере имеем:

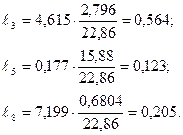
Коэффициенты эластичности так же выражены, как и β_j , в одинаковых единицах и сравнимы между собой. Ими удобнее, чем β-коэффициентами, пользоваться в планировании и прогнозировании. Вряд ли менеджер станет планировать увеличение фактора, скажем, инвестиций на 0,6 сигмы. Обычно планируют изменение факторов, если они управляемы, на столько-то процентов от достигнутого уровня. Например, если планируем увеличить затраты на гектар зерновых на 10%, оплату труда на 30%, а обеспеченность квалифицированными трактористами-машинистами на 20%, то можно ожидать изменения урожайности на 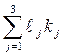, где k_j – планируемые темпы прироста факторов.

Имеем: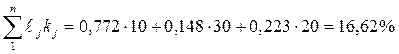

Теперь рассмотрим систему показателей тесноты многофакторных связей. Прежде всего строится матрица парных коэффициентов корреляции (табл. 1).

Таблица 1. Матрица парных коэффициентов корреляции

Признаки	y	x3	x5	x8
y	1
x3	0,860	1
x5	0,350	0,223	1
x8	0,443	0,248	0,141	1

Матрица парных коэффициентов корреляции дает исходные данные для других показателей тесноты связи и для первичной проверки на коллинеарность. В данном случае все связи между факторами слабые, коллинеарность не испортит модель.

Важнейшим показателем тесноты связи в многофакторной системе является коэффициент множественной детерминации R ² . Он измеряет общую тесноту связи вариации результативного признака y с вариацией всей системы входящих в модель факторов. Величина коэффициента множественной детерминации может быть вычислена несколькими способами.

1.Вычисление на основе матрицы парных коэффициентов корреляции

,

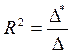где Δ^* - определитель матрицы;

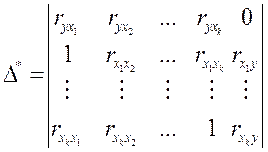, (26)

а Δ – определитель матрицы, не включающей первой строки Δ^* и ее последнего столбца, т.е.:

.

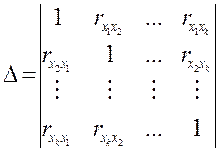При двух факторах получается упрощенная формула расчета:

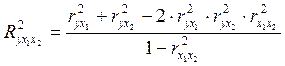(27)

Из (27) следует, что при независимости факторов друг от друга, т.е. , коэффициент множественной детерминации есть сумма парных коэффициентов детерминации.

Пользуясь формулой (27), можно вычислить три возможных двухфакторных коэффициента детерминации:

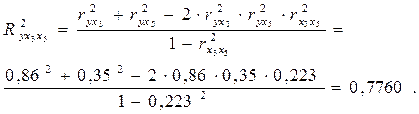
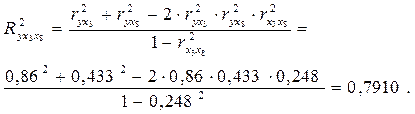
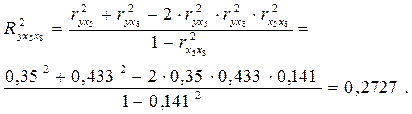
2.Вычисление на основе парных коэффициентов корреляции и β-коэффициентов:

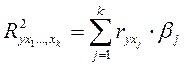(28)

В примере: R ² =0,86·0,772+0,35·0,147+0,433·0,223=0,8119.

3.Вычисление как корреляционное отношение, т.е. отношение вариации результативного признака y , связанной с вариацией системы факторов, входящих в модель (в уравнение регрессии), ко всей, общей, вариации результативного признака:

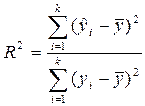. (30)

Числитель формулы (30) – это сумма квадратов отклонений индивидуальных расчетных значений результативного признака от его средней, а знаменатель – сумма квадратов фактических значений результативного признака от средней, для всех единиц совокупности.

Частными коэффициентами детерминации называются показатели, измеряющие, на какую долю уменьшается необъясненная вариация уже имеющимися в модели факторами при включении в модель данного фактора x_m . Формула частного коэффициента детерминации такова:

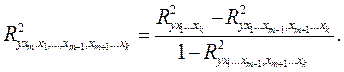(31)

В нашем примере: