Реферат: Модель оценки финансовых активов
Содержание:
1. Модель оценки финасовых активов. В- коэффициент регрессии. Безрисковый уровень доходности и премия за риск.
2. Оптимизация инвестиционного портфеля. Доходность и риск. Эффективная диверсификация портфеля.
3) Задача.
4) Список Литературы.
1) Модель оценки финансовых активов. В- коэффициент регрессии. Безрисковый уровень доходности и примия за риск.
Наряду с доходностью ценных бумаг или их портфелей, может быть определена доходность конкретного финансового рынка (например NYSE) в целом. Для этого можно использовать изменение какого-либо фондового индекса (DJIA, S&P 500 и т.п.). Прирост (снижение) этого индекса за определенный период должен быть отнесен к значению индекса на начало периода:
, где (5.6.1)
I1, I0 – значения фондовых индексов соответственно на конец и начало периода;
rm – уровень доходности рынка в целом.
Например, фактическое значение индекса S&P 500 составило на 10 мая 2000 года 1384,29, на следующий день оно достигло уровня 1401,74. Темп прироста за день (дневная доходность «средней» акции) равен 1,26%. Аннуилизировав этот результат по ставке простых процентов (временная база – 366 дней), получим:
Полученный гигантский результат отражает изменение индекса лишь за 1 день, поэтому его не стоит автоматически экстраполировать на все остальные дни года. Безусловно, рост курса акций будет чередоваться с его падением, в результате чего фактическая годовая доходность «средней» акции будет иметь гораздо более скромную величину. В табл. 5.6.1 приведена динамика фактической годовой доходности индекса S&P 500 за ряд лет в сопоставлении с динамикой доходности одной отдельно взятой акции, обращающейся на этом же рынке.
Таблица 5.6.1
| Годы | Доходность одной акции (r), % | Доходность рынка (rm), % |
| 1981 | 6,12 | 20,25 |
| 1982 | 14,97 | 13,94 |
| 1983 | 2,72 | 1,44 |
| 1984 | 13,2 | 18,41 |
| 1985 | 11,55 | 7,11 |
Приведенные в таблице данные позволяют сопоставить между собой изменения доходности отдельной акции и доходности рынка в целом. Если в предыдущем параграфе находилась теснота связи между отдельными акциями, входящими в инвестиционный портфель, то теперь можно найти степень зависимости доходности одной акции от уровня прибыльности всего рынка. В статистике подобные задачи решаются путем построения регрессионных уравнений вида:
, где (5.6.2)
y – результативный показатель;
x – влияющий фактор;
a – свободный член уравнения регрессии;
б – коэффициент регрессии;
e – погрешность.
Важнейшим параметром этого уравнения является коэффициент регрессии б, который показывает, насколько сильно изменение факторного показателя x влияет на результирующий признак y.
В случае линейной формы регрессионного уравнения, простейшим способом оценки его параметров является использование метода наименьших квадратов, заключающегося в решении относительно a: и b следующей системы линейных уравнений:
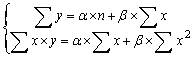, где (5.6.3)
n – общее число наблюдений (лет).
Решив ее, получим:
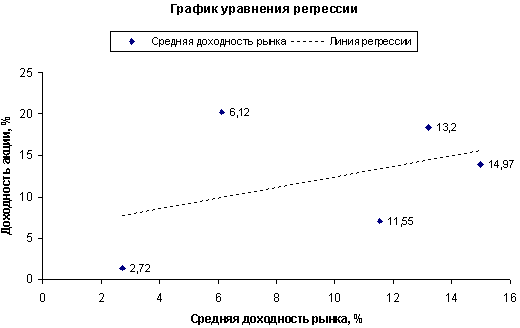
Значение коэффициента регрессии в = 0,27 показывает, что с увеличением средней доходности рынка на 1 процентный пункт, доходность данной ценной бумаги возрастет лишь на 0,27 пункта. Иными словами, акция подвержена относительно менее сильному воздействию рыночных колебаний: при снижении рыночной доходности на 1 пункт, падение доходов по этой акции также составит в среднем лишь 0,27 пункта. Графическая аппроксимация фактических данных линейной функцией представлена на рис. 5.6.1. Коэффициент регрессии в представлен на нем углом наклона линии регрессии к оси абсцисс.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--