Реферат: Моделирование дискретной случайной величины и исследование ее параметров

Выполнил:

ст.гр. РТз – 98 – 1

Чернов В.В.

Шифр 8209127

Проверил:

Карташов В. И.

____________________

Харьков 2003

Задание 1. Выполнить моделирование на ЭВМ базовой случайной величины (БСВ) Х. Получить выборки реализаций БСВ объемом n = 170, 1700. Для каждого случая найти минимальное и максимальное значения, оценить математическое ожидание и дисперсию. Сравнить полученные числовые характеристики с теоретическими значениями.

Решение

Базовой называют случайную величину, равномерно распределенную на интервале (0,1). Моделирование производится при помощи функции rnd(m) пакета MathCad 2000, возвращающей значение случайной величины, равномерно распределенной в интервале 0xm.

а) для выборки объемом 170 (рис. 1.1): Xmin = 0.0078, Xmax = 0.996.

Первый начальный момент (математическое ожидание) равен среднему арифметическому значений выборки:

М_Х = 0.502 , (1.1)

второй центральный момент (дисперсия):

D = 0.086 , (1.2)

среднеквадратичное отклонение:

s = 0.293 . (1.3)

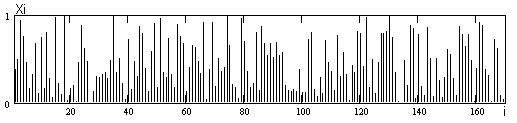
Рисунок 1.1 Выборка объемом 170.

Для выборки объемом 1700 (рис. 1.2): X_min = 0.0037, X_max = 0.998,

М_Х = 0.505 , (1.4)

D = 0.085 , (1.5)

s = 0.292 . (1.6)

Рисунок 1.2 Выборка объемом 1700.

Теоретически значения математического ожидания и дисперсии БСВ рассчиты-ваются из определения плотности распределения вероятности:

p_равн (x) = , (1.7)

математическое ожидание:

M_x = 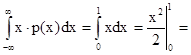0.5 , (1.8)

дисперсия:

D_x =

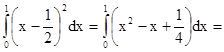
=0.083 , (1.9)

что хорошо совпадает с результатами моделирования (1.1) – (1.5).

Задание 2. Получить выборку реализаций БСВ объемом n = 1700. Построить гистограмму распределений и сравнить ее с плотностью распределения равномерно распределенной случайной величины.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--