Реферат: Нахождение корней уравнения методом простой итерации (ЛИСП-реализация)
Найдем корень уравнения
![]() .
.
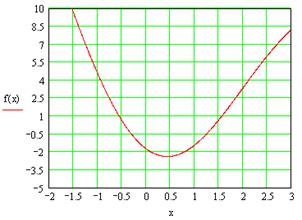
Рисунок 1. Функция ![]()
Будем искать простой корень уравнения, находящийся на отрезке локализации [-0.4,0].
Приведем уравнение к виду x=f(x), где
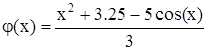 .
.
Проверим условие сходимости:
![]() .
.

Рисунок 2. График производной
Максимальное по модулю значение производной итерационной функции достигается в левом конце отрезка
![]()
![]() .
.
![]() .
.
Выполним 3 итерации по расчетной формуле
x= ![]() (x),
(x), ![]()
1 итерация ![]()
![]() .
.
2 итерация ![]()
![]() .
.
3 итерация ![]()
![]() .
.
2. Математические и алгоритмические основы решения задачи
2.1 Описание метода простых итераций
Рассмотрим уравнение
f(x)=0 (2.1)
с отделенным корнем X[a, b]. Для решения уравнения (2.1) методом простой итерации приведем его к равносильному виду:
x=φ(x). (2.2)
Это всегда можно сделать, причем многими способами. Например:
x=g(x) · f(x) + x ≡ φ(x),
где g(x) - произвольная непрерывная функция, не имеющая корней на отрезке [a,b].