Реферат: Нахождение кратчайшего пути
Свет вода газ
Можно ли так проложить коммуникации, чтобы они, нигде не пересекаясь друг с другом, соединяли каждый дом с источниками электричества, газа и воды? Иначе говоря, можно построить плоский граф с вершинами в шести указанных точках? Оказывается, такой граф построить нельзя. Об этом говорится в одной очень важной теореме – так называемой теореме Куратовского. Теорема утверждает, что каждый граф, не являющийся плоским, содержит в качестве подграфа один из двух простейших пространственных графов:
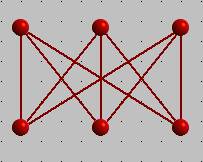
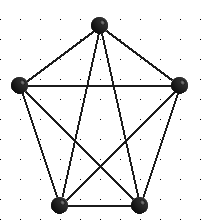
В середине 19 в. появились работы, в которых при решении практических задач были получены результаты, относящиеся к теории графов. Так, например, Г. Кирхгоф при составлении полной системы уравнений для токов и напряжений в электрической схеме предлож ил по существу представлять такую схему графом и находить в этом графе остовные деревья, с помощью которых выделяются линейно независимые системы контуров. А. Кэли , исходя и з задач подсчета числа изомеров предельных углеводородов, пришел к задачам перечисления и описания деревьев, обладающих заданными свойствами, и решил некоторые и з них.
В 20 в. задачи, связанные с графами, начали возникать не только в физике, химии, электротехнике би ологии, экономике, социологии и т.д., но и внутри математики, в таких разделах, как топология, алгебра, теория вероятностей, теория чисел. В начале 20 в. графы стали использоваться для представления некоторых математич еских объе ктов и формальной постановки различных ди скретных задач; при этом наряду с термином «граф» употреблялись и другие термины, например, карта, компле кс, диаграмма, сеть, лабиринт. После выхода в свет в 1936 году монографии Д. Кёнига термин «граф» стал более употребительным, чем другие. В этой работе были систематизированы известные к тому времени факты. В 1936 году вышла небольшая брошюра Ойстена Оре, содержащая блестящее элементарное введение в теорию графов. В 1962 году в Англии была издана книга французского математика Клода Бержа “Теория графов и её приложение”. Обе книги, безусловно, представляют интерес для любителей занимательной математики. Сотни известных головоломок, на первый взгляд не имеющих ничего общего друг с другом, легко решаются с помощью теории графов.
В 20-30-х годах 20 в. появились первые результаты, относящиеся к изучению свойств связности, планарности, симметрии графов, которые привели к формированию ряда новых направлений в теории графов.
Значительно расширились исследования по теории графов в конце 40-х - начале 50-х годов, прежде всего в силу развития кибер нетики и вычислительной техники. Благодаря развитию вычислительной техники, изучению сложных кибернетич еских систем, интерес к теории графов возрос, а проблематика теории графов существенным образом обогати лась. Кроме того, использование ЭВМ позволило решать возникающие на практике конкретные задачи, связанные с большим объемом вычислений, прежде не поддававшиеся решению. Для ряда экстремальных задач теории графов были раз работаны методы их решения, например, один из таких методов позволяет решать задачи о построении максимального потока через сеть. Для отдельных классов графов (деревья, плоские графы и т. д.), которые изучались и ранее, было показано, что решения некоторых задач для графов и з этих классов находятся проще, чем для прои звольных графов (нахождение условий существования графов с заданными свойствами, установление изоморфи зма графов и др.).
Характеризуя проблематику теории графов, можно отметить, что некоторые направления носят более комби наторный характер, другие - более геометрический. К первым относятся, например, задачи о подсчете и перечислении графов с фиксированными свойствами, задачи о построении графов с заданными свойствами. Геометрический (топологический) характе р носят многие циклы задач теории графов, например, графов обходы, графов укладки. Существуют направлени я, связанные с различными классификациями графов, например, по свойствам их разложен ия.
Примером результата о существовании графов с фиксированными свойствами может служить критери й реализуемости чисел степенями вершин некоторого графа: набор целых чисел, ![]() сумма которых четна, можно реализовать степе нями вершин графа без петель и кратных ребер тогда и только тогда, когда для любого r выполняется условие
сумма которых четна, можно реализовать степе нями вершин графа без петель и кратных ребер тогда и только тогда, когда для любого r выполняется условие ![]()
Примерами задач о подсчете графов с заданными свойствами являются задачи о нахождении количеств неизоморфных графов с одинако вым числом вершин и (или) ребер. Для числа неизоморфных деревьев с n вершинами была получена асимптотич еская формула 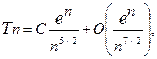 где C == 0,534948..., e == 2,95576...
где C == 0,534948..., e == 2,95576...
![]()
Для числа G n неизоморфных графов без петель и кратных ребер с n вершинами было показано, что 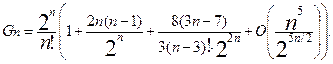
Наряду с проблемами, носящи ми общий характер, в теории графов имеются специфич еские циклы задач. В одном из них изучаются различные свойства связности графов, исследуется строение графов по свойствам связности. При анализе надежности сетей связи, э лектрон ных схем, коммуни каци онных сетей возникает задача о нахождении коли честв непересекающихся цепей, соединяющих разли чные вершины графа. З десь получен ряд результатов. Например, наи меньш ее число вершин, разделяющих две несмежные вершины графа, равно наибольшему числу непересекающихся (по вершинам) простых цепей, соединяющих эту пару вершин. Найдены критерии и построены эффективные алгоритмы установления меры связности графа (наименьшего числа вершин или ребер, удаление которых нарушает связность графа).
В другом направлении исследований теории графов изучаются маршруты, содержащие все вершины или ребра графа. Известен простой критерий существования маршрута, содержащего все ребра графа: в связ ном графе цикл, содержащий все ребра и проходящий по каждому ребру один раз, существует тогда и только тогда, когда все вершины графа имеют четные степени. В случае обхода множества вершин графа имеется только ряд достаточных условий существован ия цикла, проходящего по всем вершинам графа по о дному разу. Характерным спе ци фически м направлени ем теории графов является цикл задач, связанный с раскрасками графов, в котором изучаются разбиения множества вершин (ребе р), обладающи е определенными свойствами, например, смежные вершины (ребра) должны принадлежать различным множествам (вершины или ребра из одного множества окрашиваются одним цветом). Было доказано, что наименьшее число цветов, достаточное для раскраски ребер любого графа без петель с максимальн ой степенью a , равно Зa/2 , а для раскраски вершин любого графа без петель и кратных ребер достаточно a+1 цветов.
Существуют и другие циклы задач, некоторы е из ни х сложи лись под влиянием различных разделов математики. Так, под влиянием топологии производи тся изучение вложени й графов в разли чные поверхности. Например, было получено необходимое и достаточное условие вложения графа в плос кость (критери й П онтряг ин а - Кур атовског о см. выше): граф является плоски м тогда и только тогда, когда он не содержит п одграфов, получаемых с помощью подразби ения ребер и з полного 5-вершинного графа и полного двудольного графа с тремя вершинами в каждой доле. Под влиянием алгебры стали изучаться г руппы автоморфизмов графов. В частности, было доказано, что каждая конечная группа изоморфна группе автоморфизмов некоторого графа. Влияни е теори и вероятностей сказалось на исследовании г рафов случайных. Многие свойства были изучены для «почти всех» графов; например, было показано, ч то почти все графы с n верши нами связаны, имеют д иа ме тр 2, обла дают г ам иль тоновы м цикл ом (ци клом, проходящим через все верши ны графа по одному разу).
В теории графов существуют специфич еские методы реше ния экстремальных задач. Оди н и з них основан на теореме о максимальном потоке и ми нимальном разрезе, утверждающей, что макси мальный поток, который можно пропустить через сеть из верши ны U в вершину V , равен мини мальной пропускной способности разрезов, разделяющих вершины U и V . Были построены разли чные эффективные алгоритмы нахождения максимального потока.
Большое значени е в теории графов и меют алгоритмические вопросы. Для конечных графов, т. е. для графов с конеч ным множеством вершин и ре бе р, как прави ло, проблем а существовани я алгоритма решени я задач, в том чи сле экстремальных, решается положительно. Решени е многих задач, связанных с конечными графами, может быть выполнено с помощью полного перебора всех допустимых вариантов. Однако таким способом удается решить задачу только для графов с небольши м чи слом вершин и ребер. Поэтому существенное значени е для теории графов имеет построение эффективных алгори тмов, находящих точное или приближенное решени е. Для некоторых задач таки е алгоритмы построены, например, для установлени я планарности графов, определения изоморфизма деревьев, нахождения максимального потока.
Результаты и методы теории графов применяются при решении транспортных задач о пе ре возках, для нахождения оптимальных решений задачи о назначениях, для выделе ния « узких мест» при планировании и управлении разработок проектов, при составлении опти мальных маршрутов доставки грузов, а также при моделировании сложных технология, процессов, в построении различных дискретных устройств, в программировании и т. д.
1.2. Основные термины и теоремы теории графов .
1. Граф - Пара объектов G = ( X , Г ) ,где Х - конечное множество ,а Г –конечное подмножество прямого произведения Х*Х . При этом Х называется множеством вершин , а Г - множеством дуг графа G .
2. Любое конечное множество точек (вершин), некоторые из которых попарно соединены стрелками , (в теории графов эти стрелки называются дугами), можно рассматривать как граф.
3. Если в множестве Г все пары упорядочены, то такой граф называют ориентированным .
4. Дуга - ребро ориентированного графа.
5. Граф называется вырожденным , если у него нет рёбер.
6. Вершина Х называется инцидентной ребру G , если ребро соединяет эту вершину с какой-либо другой вершиной.
7. Подграфом G(V1 , E1 ) графа G(V, E) называется граф с множеством вершин V1 ÍV и множеством ребер (дуг) E1 Í E, - такими, что каждое ребро (дуга) из E1 инцидентно (инцидентна) только вершинам из V1 . Иначе говоря, подграф содержит некоторые вершины исходного графа и некоторые рёбра (только те, оба конца которых входят в подграф).
8. Подграфом, порождённым множеством вершин U называется подграф, множество вершин которого – U , содержащий те и только те рёбра, оба конца которых входят в U .
9. Подграф называется остовным подграфом , если множество его вершин совпадает с множеством вершин самого графа.
10. Вершины называются смежными , если существует ребро , их соединяющее.
11. Два ребра G1 и G2 называются смежными , если существует вершина, инцидентная одновременно G1 и G2 .
12. Каждый граф можно представить в пространстве множеством точек, соответствующих вершинам, которые соединены линиями, соответствующими ребрам (или дугам - в последнем случае направление обычно указывается стрелочками). - такое представление называется укладкой графа.