Реферат: Нахождение кратчайшего пути
3. В связном графе любые две простые цепи максимальной длины имеет по крайней мере одну общую вершину.
4. В графе с N вершинами и К компонентами связности число рёбер не превышает 1/2(N-K)(N-K+1).
5. Пусть у графа G есть N вершин . Пусть D(G)- минимальная из степеней вершин этого графа . Тогда D(G) > 1/2 (N-1).
29. Связный граф без циклов называется деревом .
Деревья особенно часто возникают на практике при изображении различных иерархий. Например, популярные генеалогические деревья.
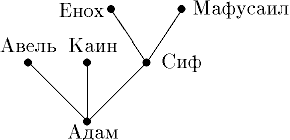
Пример(генеалогическое дерево): На рисунке показано библейское генеалогическое дерево.
Эквивалентные определения дерева.
1. Связный граф называется деревом, если он не имеет циклов.
2. Содержит N-1 ребро и не имеет циклов.
3. Связный и содержит N-1 ребро.
4. Связный и удаление одного любого ребра делает его несвязным.
5. Любая пара вершин соединяется единственной цепью.
6. Не имеет циклов и добавление одного ребра между любыми двумя вершинами приводит к появлению одного и только одного цикла.
Раскраска графов
Раскраской графа G = (V,E) называется отображение D: V ® N . Раскраска называется правильной , если образы любых двух смежных вершин различны: D (U) ≠ D (V), если (U, V) Î I. Хроматическим числом графа называется минимальное количество красок, необходимое для правильной раскраски графа.
Теорема 5.
Граф является планарным тогда и только тогда, когда он не содержит подграфа, изоморфного одному из следующих (графы Понтрягина - Куратовского).
 |  |
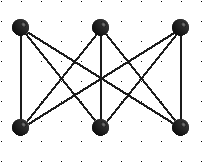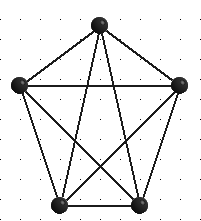???? ?33 ???? ?5
Свойство: В любом планарном графе существует вершина, степень которой<=5.
Способы задания графов:
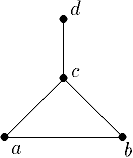1. Геометрический:
2. Матрица смежности:
|
a |
В |
c |
d | |
|
A |
0 |
1 |
1 |
0 |
|
B |
К-во Просмотров: 618
Бесплатно скачать Реферат: Нахождение кратчайшего пути
|