Реферат: Некоторые особенности психологического восприятия и визуальной интерпретации динамических процессов
Другая интересная характеристика случайных блужданий – количество времени, которое точка проводит на одной стороне графика. Выводы показывают, если количество бросков велико, то в 20% случаев наша траектория будет находиться на одной стороне 97,5% времени, а в 10% - 99,5% времени. Эти цифры говорят сами за себя.
Вышеописанные характеристики случайных блужданий, описываются известным в статистике законом Арксинуса, применительно к нашему последнему примеру – это вероятность того, какую часть от всего отведенного времени точка находится на положительной или отрицательной стороне. Равенство - 50% на положительной стороне и 50% на отрицательной (интуитивно наиболееожидаемый сценарий) – имеет наименьшую вероятность, а максимальную вероятность – сценарий, при котором вся траектория находится либо на одной, либо на другой стороне.
Общий вид распределения вероятностей в зависимости от доли времени нахождения на одной стороне вы видите на РИС.8.
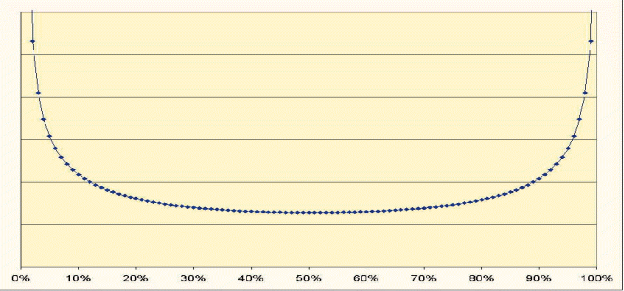 РИС.8
РИС.8
Хочу сразу оговориться, что мое выступление не следует воспринимать как критику технического анализа.
Необходимо просто более объективно воспринимать то, что мы видим в поведении цен и в результатах, которые мы получаем. Приведу пример. Многоуважаемый мною Джон Мерфи, автор наверное лучших книг по техническому анализу в главе, где он дискутирует с приверженцами теории случайных блужданий рынка, коим я ни в коей мере не являюсь, приводит график швейцарского франка за1985 год:
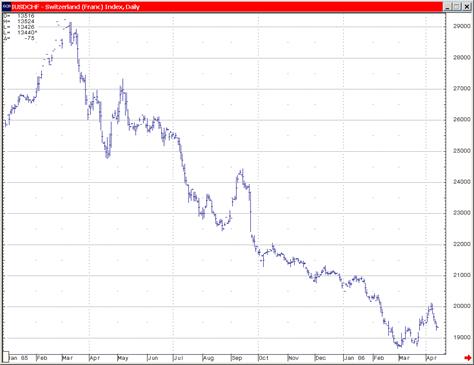
Далее он пишет: «Вот видите какой здесь тренд. О какой случайности может идти речь?» Аргумент, к сожалению, не серьезный, так как случайные блуждания выстраиваться в трендовую последовательность примерно в каждом пятом случае.
Приведу еще один пример искаженных ожиданий. В той же брокерской компании, где я играл в кости, я провел опрос среди трейдеров «Предположим мы возьмем какой-либо актив и будем каждый день подбрасывать монетку. В соответствии с тем, что выпадем орел или решка будем открывать позицию либо вверх, либо вниз. Предположим, что у нас нет комиссии и проскальзывания. Что будет происходить с нашим счетом?».
Все ответили, что счет будет колебаться вокруг нуля. Моделируем такую ситуацию. Возьмем S&P с 1991 года, дальше генерим вышеописанным способом столбец из 1 и –1, которые соответствуют длинной или короткой позициям. Посмотрим на варианты графиков сальдо нашего теоретического счета, управляемого случайной торговой системой.
 РИС.7
РИС.7
Тоже самое. Никаких колебаний вокруг 0 нет. Многие из таких траекторий будут опять же иметь тредовый вид. Растущие тренды в данном случае будут соответствовать выигрышным торговым системам.
Надо отдавать себе отчет, что если мы сделали торговую систему и положили ее на какой-то актив пусть даже с очень длинной историей, то велика вероятность, что историческое тестирование случайным образом породит замечательную траекторию EQUITY системы, но этот один эксперимент со статистической точки ничего значить не будет.
Поэтому с точки зрения создания торговых систем очень важно проверять систему на грубость: исследовать чувствительность к параметрам, тестировать на различных активах и т.д. Обо всем об этом неоднократно говорилось, и я думаю, вы прекрасно об этом знаете.
Очевидно, что поведение цен не является случайным блужданием, также как, скажем, и EQUITY конкретной торговой системы. Но надо понимать, что траектории, которые мы видим, существуют на фоне некого пространства случайных блужданий. Это пространство, при прочих равных, обладает свойствами которые сильно отличаются от наших интуитивных ожиданий и что четкое представление об этих свойствах, безусловно, необходимо для того, чтобы объективно оценивать то, чем мы с вами занимаемся.