Реферат: Некоторые парадоксы теории относительности

Пусть в системе отсчета в начальный момент в точке, совпадающей с началом координат произошла вспышка света. В последующий момент времени фронт световой волны, в силу закона постоянства скорости света, распространился до сферы радиуса с центром в начале координат системы . Однако в соответствии с постулатами Эйнштейна, это же явление мы можем рассмотреть и точки зрения системы отсчета , движущейся равномерно и прямолинейно вдоль оси , так, что ее начало координат и направления всех осей совпадали в момент времени с началом координат и направлениями осей первоначальной системы . В этой движущейся системе, соответственно постулатам Эйнштейна, за время свет также распространится до сферы радиуса

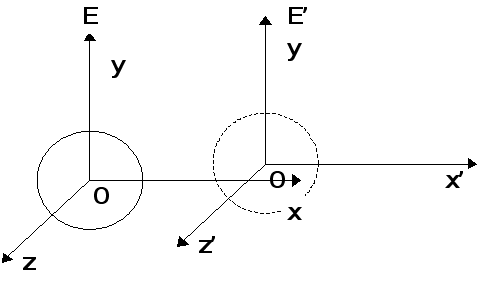
радиуса , однако, в отличие о предыдущей сферы должен лежать в начале координат системы , а не . Несовпадение этих сфер, т.е. одного и того же физического явления, представляется чем-то совершенно парадоксальным и неприемлемым с точки зрения существующих представлений. Кажется, что для разрешения парадокса надо отказаться от принципа относительности, либо от принципа постоянства скорости света. Теория относительности предлагает, однако, совершенно иное разрешение парадокса, состоящее в том, что события, одновременные в одной системе отсчета , неодновременны в другой, движущейся системе , и наоборот. Тогда одновременные события, состоящие в достижении световым фронтом сферы, определяемой уравнением

, не являются одновременными с точки зрения системы , где одновременны другие события, состоящие в достижении тем же световым фронтом точек сферы, определяемой уравнением

Таким образом, одновременность пространственно разобщенных событий перестает быть чем-то абсолютным, как это принято считать в повседневном макроскопическом опыте, а становится зависящей от выбора системы отсчета и расстояния между точками, в которых происходит события. Эта относительность одновременности пространственно разобщенных событий свидетельствует о том, что пространство и время тесно связаны друг с другом, т.к. при переходе о одной системе отсчета к другой, физически эквивалентной, промежутки времени между событиями становятся зависящими от расстояний (нулевой промежуток становится конечным и наоборот).

Итак, постулаты Эйнштейна помогли нам прийти к новому фундаментальному положению в физической теории пространства и времени, положению о тесной взаимосвязи пространства и времени и об их нераздельности, в этом и состоит главное значение постулатов Эйнштейна.

Основное содержание теории относительности играет постулат о постоянстве скорости света. Основным аргументов в пользу этого является та роль, которую отводил Эйнштейн световым сигналам, с помощью которых устанавливается одновременность пространственно разобщенных событий. Световой сигнал, распространяющийся всегда только со скоростью света, приравнивается, таким образом, к некоторому инструменту, устанавливающему связь между временными отношениями в различных системах отсчета, без которого якобы понятия одновременности разобщенных событий и времени теряют смысл. Необходимость такого истолкования содержания теории относительности легко доказывается, если обратиться к одному из возможных выводов преобразований Лоренца, опирающемуся на постулат относительности и вместо постулата о постоянстве скорости света использующему лишь допущение о зависимости массы тела от скорости.

Вывод преобразований Лоренца без постулата о постоянстве скорости света.

Для вывода преобразований Лоренца будем опираться лишь на “естественные” допущения о свойствах пространства и времени, содержавшиеся еще в классической физике, опиравшейся на общие представления, связанные с классической механикой:

1. Изотропность пространства, т.е. все пространственные направления равноправны.

2. Однородность пространства и времени, т.е. независимость свойств пространства и времени от выбора начальных точек отсчета (начала координат и начала отсчета времени).

3. Принцип относительности, т.е. полная равноправность всех инерциальных систем отсчета.

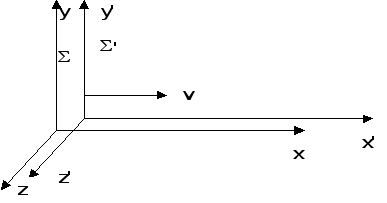
Различные системы отсчета по-разному изображают одно и то же пространство и время как всеобщие формы существования материи. Каждое из этих изображений обладает одинаковыми свойствами. Следовательно, формулы преобразования, выражающие связь между координатами и временем в одной - “неподвижной” системе с координатами и временем в другой - “движущейся” системе , не могут быть произвольными. Установим те ограничения, которые накладывают “естественные” требования на вид функций преобразования:

1. Вследствие однородности пространства и времени преобразования должны быть линейными.

Действительно, если бы производные функций по не были бы константами, а зависели от то и разности , выражающие проекции расстояний между точками 1 и 2 в “движущейся” системе, зависели бы не только от соответствующих проекций , в “неподвижной” системе, но и от значений самих координат что противоречило бы требованию независимости свойств пространства от выбора начальных точек отсчета. Если положить, что проекции расстояний вида x‘ = = зависят только от проекций расстояний в неподвижной системе, т.е. от x = , но не зависит от , то

при т.е. или .

Аналогично можно доказать, что производные по всем другим координатам также равны константам, а следовательно, и вообще все производные по суть константы.

2. Выберем "движущуюся" систему таким образом, чтобы в начальный момент точка, изображающая ее начало координат, т.е. совпадала с точкой, изображающей начало координат "неподвижной" системы, т.е. , а скорость движения системы была бы направлена только по

Если мы также учтем требование изотропности пространства, то линейные преобразования для системы отсчета , выбранной указанным образом, запишутся в виде Здесь отсутствуют члены, содержащие и в выражениях и , в силу изотропности пространства и наличия единственного выделенного направления вдоль оси , соответственно постановке задачи. На этом же основании в выражениях для и отсутствуют члены, пропорциональные, соответственно, и , а коэффициенты при и одинаковы. Члены, содержащие и , отсутствуют в выражениях для и в силу того, что ось все время совпадает с осью . Последнее было бы невозможно, если бы и зависели от и .

3. Изотропность предполагает также симметричность пространства. В силу же симметрии ничто не должно измениться в формулах преобразования, если изменить знаки и , т.е. одновременно изменить направление оси и направление движения системы . Следовательно, (d) Сравнивая эти уравнения с предыдущими () получаем:

. Вместо удобно ввести другую функцию , так, чтобы выражалось через ипосредством соотношения Согласно этому соотношению, - симметричная функция. Используя это соотношение, преобразования (d) можно записать в виде (e), причем все входящие в эти формулы коэффициенты суть симметрии функции .

4. В силу принципа относительности обе системы, "движущаяся" и "неподвижная", абсолютно эквивалентны, и поэтому обратные преобразования от системы кдолжны быть тождественно прямым от к. Обратные преобразования должны отличаться лишь знаком скорости , т.к. системадвижется относительно системывправо со скоростью , а система движется относительно системы (если последнюю считать неподвижной), влево со скоростью . Следовательно, обратные преобразования должны иметь вид . (f) Сравнивая эти преобразования с (e), получаем . Но в силу симметрии получаем, что , т.е. . Очевидно, имеет смысл лишь знак (+), т.к. знак (-) давал бы при перевернутую по и систему. Следовательно . Замечая, что коэффициенты - тоже симметричные функции , первое и последнее уравнение из (e) и (f) можно записать в виде: А) , а) , В) , в) . Умножая А) на , В) на и складывая, получим . Сравнивая это выражение с а), получаем . Откуда имеем

Следовательно, извлекая квадратный корень и замечая, что знак (-) так же, как и для , не имеет смысла, получаем . Итак преобразования приобретают вид: (g) или ,подробнее: ,(h) где - неизвестная пока функция .

5. Для определения вида обратимся вновь к принципу относительности. Очевидно, что преобразования (g) должны быть универсальными и применимыми при любых переходах от одних систем к другим. Таким образом, если мы дважды перейдем от системык и от к , то полученные формулы, связывающие координаты и время в системе с координатами и временем в, должны также иметь вид преобразований (g). Это вытекающее из принципа относительности требование, в совокупности с предыдущими требованиями обратимости, симметрии и т.д. означает, что преобразования должны составлять группу.

Воспользуемся этим требованием групповости преобразований. Пусть - скорость системы относительнои - скорость системы относительно системы

Тогда согласно (g)

Выражая и через и , получаем

Согласно сформулированному выше требованию эти же преобразования должны записываться в виде (g), т.е. (k) Коэффициенты, стоящие при в первой из этих формул и при во второй, одинаковы. Следовательно, в силу тождественности предыдущих формул и этих, должны быть одинаковы и коэффициенты, стоящие при в первой из предыдущих формул и приво второй из формул (h) т.е. . Последнее равенство может быть удовлетворено только при

6. Итак, в преобразованиях (h) h является константой, имеющей размерность квадрата скорости. Величина и даже знак этой константы не могут быть определены без привлечения каких-либо новых допущений, опирающихся на опытные факты.