Реферат: Нелинейное программирование
– Их счастье, если по дну оврага протекает ручей. А если родник в самой низкой точке?
– Да, тогда судьбе Гаусса и Зейделя не позавидуешь: идя на восток, они придут в точку A – это самое низкое место на их пути. А в направлении север-юг самая низкая точка – это снова точка A. Таким образом, бедняги придут к выводу, что A – самая низкая точка на местности и умрут в ней от жажды.
– Но может быть, их спасёт фляжка Коши?
– Боюсь, что и фляга Коши останется пустой, если он встретится с оврагом. Оказавшись у дна оврага, он будет искать направление самого крутого спуска, и оно неизбежно приведёт его в точку по другую сторону оврага. Из этой точки он вернётся на прежнюю сторону и дальше пойдёт небольшими шажками до тех пор, пока жажда не свалит его. Ведь весь овраг он увидеть не может – его фонарь способен осветить местность лишь у самых ног. Надо придумать что-нибудь другое...
– А что если Канторович достигнет цели? Хотя не думаю: если овраг искривлён, а овраги редко бывают прямыми, то он начнёт метаться по дну оврага, почти не приближаясь к цели. Надо стараться двигаться по дну оврага.
– Разумеется, но как? Впрочем... кажется, придумал. Посмотрите на рисунок 4. Давайте мы оба, вы и я, пойдём из двух разных точек методом Канторовича. Скажем, я отсюда, а вы – отойдя шагов на сто в любом направлении.
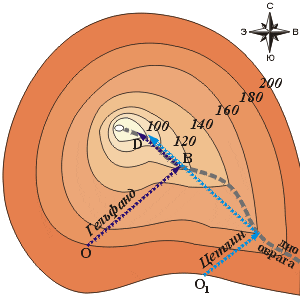
Рис. 4
– Понятно, а дальше? Ага, дальше мы оба спустимся на дно оврага и постараемся увидеть фонари друг друга. Допустим, нам это удастся. Тот из нас, чей фонарь выше, двинется по направлению к тому, чей фонарь ниже.
– Но встретившись, не остановится, а пройдет дальше в том же направлении до точки D. Из этой точки он снова спустится на дно оврага, и мы опять попытаемся увидеть друг друга. И так до тех пор, пока уровень на дне оврага не укажет горизонтальный участок.
И, выбрав фонари поприметнее, оба отправились каждый своим путём.
– А вы, я вижу, не торопитесь к влаге? – спросил Растригина Винер. – Иначе почему бы вам не воспользоваться одним из весьма разумных способов, которые предложили наши друзья по несчастью?
– У всех этих способов один недостаток – слишком много приходится возиться с уровнем, пока найдёшь нужное направление. А что если пойти по какому-либо направлению наугад, пока оно ведёт на спуск? Потом изменить направление и снова спускаться по нему. Изменить, разумеется, тоже наугад. Разве таким образом я не приду к цели? Стоит ли терять время на отыскание направления наискорейшего спуска, если уже через несколько шагов оно перестает им быть?
И не успел Винер возразить или согласиться, как Растригин закрыл глаза, повернулся несколько раз на месте, как делают при игре в жмурки, и отправился в темноту.
Методы спуска
Необходимость найти максимум или минимум (объединяемых названием «экстремум» – «крайнее значение») некоторой функции возникает во многих задачах экономики и техники. А местность можно считать макетом функции двух переменных, скажем широты и долготы. Значение функции – это высота местности (над уровнем моря) в данной точке, горизонтали – линии уровня, вдоль них функция постоянна. И ситуация, возникающая при поиске экстремума, во многом сходна с той, в которой оказались неудачливые путешественники. Поиск экстремума происходит как бы в темноте, единственным средством ориентации служат значения минимизируемой (максимизируемой) функции в какой-то точке, а также направления её наискорейшего убывания или возрастания.
Придумано уже немало методов отыскания экстремума. Не случайно, как заметил читатель, фамилии потерпевших кораблекрушение совпадают с фамилиями ряда математиков прошлого и настоящего, которые решали эту проблему. А путь, которым они отправились, показывает сущность их методов отыскания экстремума.
Великий француз П.Ферма (1601–1665) первым ясно осознал и сумел описать аналитически свойство экстремума гладкой непрерывной функции: касательная в этом месте должна быть горизонтальна. К.Гаусс (1777–1855) и А.Зейдель (1821–1896), следуя своему методу покоординатного спуска, по очереди спускались то вдоль одной, то вдоль другой координаты. Спускались до тех пор, пока касательная к направлению движения не станет горизонтальной. А положение уровня естественно определяет направление касательной.
Обратите внимание на то, что Гаусс и Зейдель не стремились спускаться по тому направлению, где крутизна больше всего. К этой идее первым пришёл О.Коши (1789–1857). Вектор, указывающий направление (вверх) с наибольшей крутизной, называется градиентом, а сам метод Коши – градиентным методом. Именно по градиенту стал бы прокладывать свой путь Коши, если бы его целью была самая высокая точка местности, чтобы осмотреться. Но вспомним, что на острове стояла мгла кромешная и целью Коши была вода. Поэтому он отправился по направлению наискорейшего убывания высоты местности, или по направлению антиградиента. Для определения антиградиента функции существуют точные и приближённые методы, но нам достаточно представить себе уровень, который мы прикладываем к земле и разыскиваем то направление, при котором воздушный пузырёк быстрее всего убегает к краю шкалы. Конечно, способ этот весьма неточен, да и мороки с ним немало. Но и для определения градиента с помощью упомянутых аналитических методов тоже приходится повозиться.
А потому нетрудно понять наших современников, японцев С.Иномату и М.Кумаду, которые попытались придать процессу спуска по антиградиенту вышеописанный физический смысл. Между прочим, их метод так и назвали «методом тяжёлого шарика». Только разумеется, при его использовании не катают глобус по макету функции, а лишь решают дифференциальные уравнения движения.
Немало трудностей ждёт того, кто ищет экстремум функции, но одна из самых коварных – это овраги. Любой из методов, даже наиболее совершенный в вычислительном отношении метод наискорейшего спуска Л.В.Канторовича, известного советского математика, приводит к беспомощному метанию по дну оврага. Поэтому советские математики И.М.Гельфанд и М.Л.Цетлин и предложили «овражный поиск», который позволяет выследить дно оврага. Итак, как мы видим, почти все численные методы поиска наилучшего направления спуска так или иначе связаны с антиградиентом. Правда, оказалось, что труды по отысканию антиградиента не всегда вознаграждаются качеством найденного направления спуска, и советский учёный Л.А.Растригин предложил вообще не тратить сил и машинного времени на поиск антиградиента, а шагать куда себе вздумается, то бишь по случайному направлению. И представьте, результаты такого образа действий оказались ничуть не хуже в вычислительном отношении, чем поиски наилучших путей. Иначе говоря, не настолько эти наилучшие пути превосходят по качеству случайный, чтобы стоило тратить время на их поиск. Разумеется, чтобы выбрать направление спуска случайным образом, не крутятся на месте с закрытыми глазами – для этого в машине используют датчики случайных чисел. И вообще численную сторону методов нелинейного программирования трудно продемонстрировать на бумаге – это существенно машинные методы.
Но вернёмся к потерпевшим кораблекрушение и узнаем, кому из них сопутствовал успех в поиске воды.
Там, за перевалом
Итак, все разбрелись в поисках воды, кроме кучки Скептиков.
– Дьявольская жажда! – промолвил один из них. – Неужели вас она не мучит?
– Не меньше, чем вас, – ответил Винер от имени остальных. – И я охотно двинулся бы на поиски воды, если бы меня убедил какой-то из предложенных способов. Но увы! Если мы начнём таким способом искать высшую точку Земли, то вместо Эвереста окажемся на вершине соседнего холмика. И самое ужасное то, что у нас нет никакого средства отличить этот холмик от Эвереста. Если, конечно, не привлечь на помощь математике обыкновенную географию.
– Как это нет? Почему? – поинтересовался молодой Скептик, которого скептицизм не отучил ещё задавать вопросы.
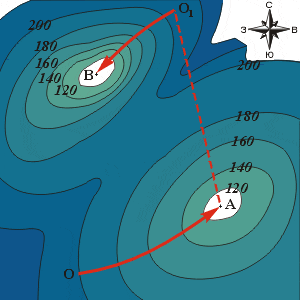
– Очень просто. С помощью фонарика мы способны лишь убедиться, что из данной точки пути ведут вниз. А что там, дальше? Вот тут наши друзья предложили ряд способов, – он снисходительно показал на оставшиеся листки из судового журнала. – Они исходили из того, что на острове только одна низина. А если их много, и вода лишь в самой низкой из этих низин (рис. 5)? Спуск приведёт нас в точку A, а вода в точке B – там гуще горизонтали и, следовательно, ниже отметка. Задумайтесь над этим.