Реферат: Несостоятельность теории электромагнетизма

Из чего следует, что если уравнение задано в виде соотношения для действия на искомый вектор оператора "rot" , то из этого уравнения можно получить в качестве решения только вихревой вектор как интеграл по замкнутому контуру.

Если задано уравнение в виде действия на вектор операторов "div" или "grad div" , то из этого уравнения можно получить в качестве решения только скаляр или вектор градиентного поля.

Приложение полученных результатов исследования классической теории поля к системе уравнений электродинамики Максвелла

Рассмотрим полную систему уравнений электродинамики Максвелла для электрических и магнитных полей в вакууме с позиции основных положений классической теории поля. С этой целью перепишем полную систему уравнений для электрических и магнитных полей.

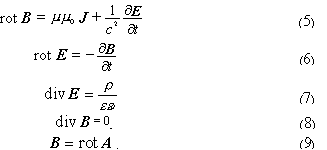
С позиции классической теории поля:

1) вектор магнитной индукции B представлен в уравнениях (5;6;8;9) данной системы уравнений, из которых видно, что вектор B носит строго вихревой характер (6;8;9), и его источники (возбудители) в исследуемом пространстве заданы уравнением (5). Т.е. поле вектора B соответствует основной задаче теории поля и может быть однозначно получено как решение данной системы уравнений после подстановки соответствующих краевых и начальных условий;

2) вектор напряженности электрического поля E , согласно уравнениям (6) и (7) данной системы, имеет отличные от нуля и дивергенцию, и ротор и, следовательно, имеет отличные от нуля вихревую и градиентную составляющие. Т.е., должен быть представлен в общем виде согласно теореме Гельмгольца (с изменением знака перед потенциальной частью):

E = - grad j + rot P ;

и

где P - некий векторный потенциал вихревой составляющей электрического поля, физический смысл которого будет выяснен дальше.

Анализируя уравнения (5) и (6), приходим к выводу, что они дают соотношения для действий оператора " rot " на векторы полей B и E , и, как было показано ранее, нетривиальные решения этих уравнений можно получить только для векторов вихревых полей. Но, т.к. вектор E имеет и вихревую, и градиентную составляющие, то решением уравнений (5) и (6) может быть только вихревая составляющая вектора E , т.е. rotP . градиентная составляющая вектора E может быть определена только из уравнения (7). Но, очевидно, уравнение (7) описывает только статические электрические поля или поля, распространяющиеся с бесконечной скоростью, что лишено всякого физического смысла. Отсюда следует, что система уравнений электродинамики Максвелла не содержит в себе описание нестационарных градиентных электрических полей и механизма их распространения.

Для того, чтобы убедиться в правильности подобных рассуждений, проделаем весь путь традиционного метода решения системы уравнений электродинамики.

Решение системы уравнений электродинамики

Подставим в уравнение (5) системы уравнений электродинамики вектор E в общем виде:

Уравнение (10) устанавливает связь между вектором rotB (имеющим строго вихревой характер) и векторами, составляющими правую часть уравнения (10). Однако очевидно, что в не╖ входят векторы имеющие как вихревой, так и градиентный характер. Но, сумма двух градиентов не может быть ротором, и, следовательно, сумма градиентных составляющих векторов, входящих в правую часть уравнения (10), равна нулю, а, значит, и не участвует в возбуждении поля магнитной индукции B . Т.е., один из основных постулатов электромагнетизма Максвелла - предположение способности изменяющегося во времени электрического поля конденсатора, имеющего в том числе и градиентную составляющую, возбуждать в окружающем пространстве магнитное поле, вступает в противоречие, в части градиентной составляющей, с фундаментальными положениями классической теории поля, являющейся на сегодняшний день основной формой записи уравнений электродинамики. Анализ литературных источников показал, что нет ни одного экспериментального подтверждения гипотезы Максвелла о возбуждении магнитного поля изменяющейся во времени градиентной составляющей электрического поля конденсатора ("Токи смещения"). Автору настоящей работы известны попытки экспериментальной проверки данной гипотезы на кафедре общей физики МГПИ им. Ленина профессором Маловым Н.Н. (ныне покойным). В результате проведенных экспериментальных исследований профессор Малов Н.Н. пришел к выводу о невозможности обнаружения магнитного поля, возбуждаемого изменяющейся во времени градиентной составляющей электрического поля конденсатора, из- за наличия магнитного поля токов, текущих по пластинам конденсатора. Вс╖ ранее сказанное дает основание для утверждения того, что гипотеза Максвелла о возбуждении магнитного поля изменяющимся во времени электрическим полем конденсатора неверна в части градиентной составляющей, как не получившая экспериментального подтверждения и противоречащая основным положениям классической теории поля, и, следовательно, уравнение (10) нужно переписать с учетом предыдущих замечаний. Т.е.:

Из данного уравнения следует, что источником магнитного поля являются строго вихревые электрические токи J и изменяющаяся во времени вихревая составляющая (rotP ) электрической напряженности E .

Необходимо также заметить, что "выпавшие" из уравнения (11) градиентные составляющие векторов J и E сохраняют свое соотношение, имеют место быть в теории электричества, но рассмотрение физических процессов, связанных с ними, выходит за рамки данной работы, как не относящееся к вопросам магнетизма непосредственно.

Из уравнения (6) полной системы уравнений электродинамики следует, что источником электрического поля E является изменяющееся во времени поле магнитной индукции B . Перепишем уравнение (6), представив вектор E в общем виде:

но , т.к.

то из уравнения (12) получаем, с учетом замечания:

Т. е., изменяющееся во времени поле магнитной индукции B является источником только вихревой составляющей (rotP ) вектора электрической напряженности E . Но, согласно уравнению (9) полной системы уравнений электродинамики :

и, следовательно,

Откуда,