Реферат: Новые формулы для вычисления планковских единиц
mpl =(Ee α2 /4πR∞ G)1/2
Из приведенных формул видно, что константы lpl , tpl , mpl выражаются с помощью других фундаментальных констант компактными соотношениями. В числе констант, с помощью которых представлены эти постоянные, использованы такие константы: фундаментальный квант hu , скорость света c, постоянная тонкой структуры α, гравитационная константа G, число π, фундаментальная метрика пространства-времени (lu , tu ), элементарная масса me , большое космологическое число Do [5,6], константа Ридберга R∞ , магнетон Бора μB , постоянная Хаббла H0 , энергия покоя электрона Ee , масса Метагалактики MU , элементарный заряд e, энергия Хартри Eh , константа фон Клитцинга RK .
2. НОВЫЕ ЗНАЧЕНИЯ ПЛАНКОВСКИХ ЕДИНИЦ
Каждая группа математических соотношений, приведенных выше, дает практически одинаковые значения lpl , tpl , mpl .Ниже приведены результаты расчета значений констант lpl , tpl , mpl , полученных по приведенным формулам. При расчетах использовались новые значения гравитационной константы G и константы Хаббла H0 [5,7], полученные с помощью универсальных суперконстант. Наиболее точные расчетные значения констант lpl , tpl , mpl , которые следуют из полученных формул:
lpl =1,616081387(45)•10-35 m
tpl =5,39066725(15)•10-44 s
mpl =2,17666773(22)•10-8 kg.
Отличия от этих значений очень незначительные и наблюдаются в седьмом-восьмом знаках, что связано с различной точностью тех констант, посредством которых представлены константы lpl , tpl , mpl :
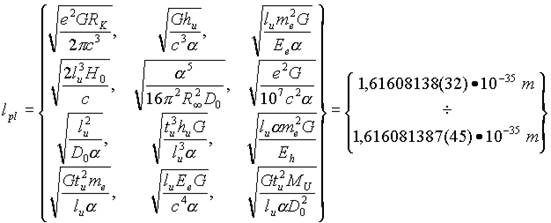
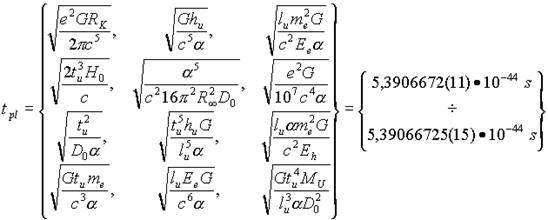
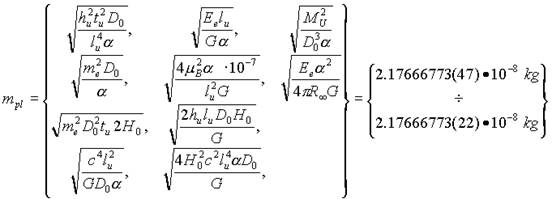
В таблицах 1, 2, 3 приведены значения планковских единиц, полученных по приведенным выше формулам:
Табл.1. Расчетные значения планковской массы.
| Кем и когда получено | Формула | Значение |
| Planck, 1900, | mpl =(ћc/G)1/2 | ~2,16•10-8 kg |
| CODATA, 1986 | 2,17671(14)•10-8 kg | |
| CODATA, 1998 | 2,1767(16)•10-8 kg | |
| Kosinov, 2000 | mpl =hu tu (Do /α)1/2 /lu 2 | 2,17666773(29)•10-8 kg |
| Kosinov, 2000 | mpl =me Do (tu •2 H0 )1/2 | 2,17666773(32)•10-8 kg |
| Kosinov, 2000 | mpl =me (Do /α)1/2 | 2,17666773(22)•10-8 kg |
| Kosinov, 2000 | mpl =(c2 lu /G) (1/Do α)1/2 | 2,17666773(34)•10-8 kg |
| Kosinov, 2000 | mpl =(Ee lu /Gα)1/2 | 2,17666773(24)•10-8 kg |
| Kosinov, 2000 | mpl =(2μB /lu ) (α•10-7 /G)1/2 | 2,17666773(25)•10-8 kg |
| Kosinov, 2000 | mpl =(2hu lu Do H0 /G)1/2 | 2,17666773(33)•10-8 kg |
| Kosinov, 2000 | mpl =(2H0 clu 2 /G) (αD0 )1/2 | 2,17666773(47)•10-8 kg |
| Kosinov, 2000 | mpl =MU (1/Do 3 α)1/2 | 2,17666773(47)•10-8 kg |
| Kosinov, 2000 | mpl =(Ee α2 /4πR∞ G)1/2 | 2,17666773(23)•10-8 kg |
Табл.2. Расчетные значения планковской длины.
| Кем и когда получено | Формула | Значение |
| Planck, 1900, | lpl =(Gћ/c3 )1/2 | ~1,61•10-35 m |
| CODATA, 1986 | 1,61605(10)•10-35 m | |
| CODATA, 1998 | 1,6160(12)•10-35 m | |
| Kosinov, 2000 | lpl =(lu 2 /D o α )1/2 | 1,616081387(51)•10-35 m |
| Kosinov, 2000 | lpl =(2lu 3 H0 /c)1/2 | 1,616081387(68)•10-35 m |
| Kosinov, 2000 | lpl =(Gtu 2 me /lu α)1/2 | 1,61608138(21)•10-35 m |
| Kosinov, 2000 | lpl =(Ghu /c3 α)1/2 | 1,61608138(18)•10-35 m |
| Kosinov, 2000 | lpl =(α5 /16π2 R∞ 2 Do )1/2 | 1,616081387(45)•10-35 m |
| Kosinov, 2000 | lpl =(tu 3 hu G/lu 3 α)1/2 | 1,61608138(18)•10-35 m |
| Kosinov, 2000 | lpl =(lu Ee G/c4 α)1/2 | 1,61608138(21)•10-35 m |
| Kosinov, 2000 | lpl =(lu me 2 G/Ee α)1/2 | 1,61608138(31)•10-35 m |
| Kosinov, 2000 | lpl =(e2 G/c2 107 α)1/2 | 1,61608138(18)•10-35 m |
| Kosinov, 2000 | lpl =(e2 GRK /2 πc3 )1/2 | 1,61608138(17)•10-35 m |
| Kosinov, 2000 | lpl =(lu αme 2 G/Eh )1/2 | 1,61608138(31)•10-35 m |
| Kosinov, 2000 | lpl =(Gtu 2 MU /D0 2 lu α)1/2 | 1,61608138(32)•10-35 m |
Табл.3. Расчетные значения планковского времени.
| Кем и когда получено | Формула | Значение |
| Planck, 1900, | tpl =(Gћ/c5 )1/2 | ~5,35•10-44 s |
| CODATA, 1986 | 5,39056(34)•10-44 s | |
| CODATA, 1998 | 5,3906(40)•10-44 s | |
| Kosinov, 2000 | tpl =(tu 2 /D o α )1/2 | 5,39066725(18)•10-44 s |
| Kosinov, 2000 | tpl =(2tu 3 H0 )1/2 | 5,39066725(23)•10-44 s |
| Kosinov, 2000 | tpl =(Gtu me /c3 α)1/2 | 5,39066725(68)•10-44 s |
| Kosinov, 2000 | tpl =(Ghu /c5 α)1/2 | 5,39066725(58)•10-44 s |
| Kosinov, 2000 | tpl =(α5 /c2 16π2 R∞ 2 Do )1/2 | 5,39066725(15)•10-44 s |
| Kosinov, 2000 | tpl =(tu 5 hu G/lu 5 α)1/2 | 5,39066725(58)•10-44 s |
| Kosinov, 2000 | tpl =(lu Ee G/c6 α)1/2 | 5,39066725(68)•10-44 s |
| Kosinov, 2000 | tpl =(lu me 2 G/c2 Ee α)1/2 | 5,3906672(11)•10-44 s |
| Kosinov, 2000 | tpl =(e2 G/c4 107 α)1/2 | 5,39066725(58)•10-44 s |
| Kosinov, 2000 | tpl =(e2 GRK /2 πc5 )1/2 | 5,39066725(55)•10-44 s |
| Kosinov, 2000 | tpl =(lu αme 2 G/c2 Eh )1/2 | 5,3906672(11)•10-44 s |
| Kosinov, 2000 | tpl =(Gtu 4 MU /D0 2 lu 3 α)1/2 | 5,3906672(11)•10-44 s |
Таким образом, за столетний период своего существования, константы lpl , tpl , mpl прошли несколько этапов, на которых их значения считались то более точными, то менее точными:
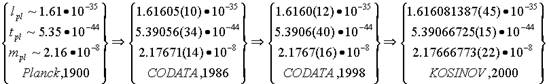
Все расчетные значения планковских единиц, полученные по новым формулам, чрезвычайно близки между собой. Все онина несколько порядков точнее значений, рекомендованных и CODATA 1986, и CODATA 1998. Совершенно очевидно, что каждая группа формул должна давать одинаковые значения констант lpl , tpl , mpl . Сближение расчетных значений, полученных по приведенным формулам, будет происходить по мере уточнения значений фундаментальных физических констант.
Соотношения вида:
lpl =(lu 2 /Do α)1/2 =(2lu 3 H0 /c)1/2 =Gtu 2 me /lu α)1/2 =(Ghu /c3 α)1/2 =(α5 /16π2 R∞ 2 Do )1/2 =(tu 3 hu G/lu 3 α)1/2 = (lu Ee G/c4 α)1/2 = (lu me 2 G/Ee α)1/2 =(e2 G/c2 107 α)1/2 =lu me /mpl α=(lu αme 2 G/Eh )1/2 =(Gtu 2 MU /D0 2 lu α)1/2 ,
tpl =(tu 2 /Do α)1/2 =(2tu 3 H0 )1/2 =(Gtu me /c3 α)1/2 =(Ghu /c5 α)1/2 =(α5 /c2 16π2 R∞ 2 Do )1/2 =(tu 5 hu G/lu 5 α)1/2 =(lu Ee G/c6 α)1/2 = (lu me 2 G/c2 Ee α)1/2 =(e2 G/c4 107 α)1/2 =(lu αme 2 G/c2 Eh )1/2 =(Gtu 4 MU /D0 2 lu 3 α)1/2 =(e2 GRK /2πc5 )1/2 ,
mpl =hu tu (Do /α)1/2 /lu 2 =me Do (tu •2 H0 )1/2 =me (Do /α)1/2 = =(c2 lu /G) (1/Do α)1/2 =(Ee lu /Gα)1/2 =(2μB /lu ) (α•10-7 /G)1/2 = (2hu lu Do H0 /G)1/2 =(2H0 clu 2 /G) (αD0 )1/2 =MU (1/Do 3 α)1/2 = (Ee α2 /4πR∞ G)1/2 можно использовать для согласования значений большого количества физических и астрофизических констант.
ВЫВОДЫ
- Найдены новые формулы для вычисления планковских единиц с помощью фундаментальных физических констант и космологических констант.
- Получены 12 эквивалентных формул для вычисления константы lpl , 12 эквивалентных формул для вычисления константы tpl , 10 эквивалентных формул для вычисления константы mpl .
- Формулы позволили получить расчетные значения констант lpl , tpl , mpl , которые на несколько порядков точнее рекомендованных значений.
- Каждая группа формул дает практически одинаковые значения планковских единиц. Различия очень незначительные и наблюдаются в седьмом-восьмом знаках, что связано с различной точностью тех констант, посредством которых представлены планковские константы lpl , tpl , mpl .
- Наиболее точные расчетные значения планковских единиц:
lpl =1,616081387(45)•10-35 m
tpl =5,39066725(15)•10-44 s
mpl =2,17666773(22)•10-8 kg.
ЛИТЕРАТУРА
1. N. Kosinov. “Five FundamentalConstants of Vacuum, Lying in the Base of allPhysicalLaws, Constants and Formulas”. PhysicalVacuum and Nature, N4, (2000).
2. Косинов Н.В. Пять универсальных суперконстант, лежащих в основе всех фундаментальных констант, законов и формул физики и космологии. Актуальные проблемы естествознания начала века. Материалы международной конференции 21 - 25 августа 2000 г., Санкт-Петербург, Россия. СПб.: "Анатолия", 2001, с. 176 - 179.