Реферат: О происхождении “высокотемпературных” осцилляций кинетических коэффициентов в висмуте и полуметаллических сплавах на его основе

Ю. А. Богод

Рассмотрен квантовый кинетический эффект, наблюдаемый вплоть до температур, близких к температуре кипения жидкого азота («высокотемпературные осцилляции»). Обсуждаются альтернативные модели, объясняющие происхождение эффекта.

“Высокотемпературные” осцилляции (ВТО) вначале наблюдались при изучении магнетосопротивления висмута и его сплавов[1-8], а затем при измерении термоэдс висмута [9,14] (в итоговом списке публикаций, касающемся ВТО, статьи следуют в хронологическом порядке). Подобно осцилляциям Шубникова-де Гааза (D. Shoenberg, F.A.S. Magnetic Oscillations in Metals. Cambridg University Press (1984)) и магнетофононному резонансу (Р.В. Парфеньев, Г.И. Харус, И.М. Цидильковский, С.С. Шалыт, УФН 112, 3 (1974); Р.В.Поморцев, А.И. Пономарев, Г.И.Харус, И.М. Цидильковский, ЖЭТФ 54, 1347 (1968)), ВТО обусловлены квантованием уровней энергии в магнитном поле, однако данный тип осцилляций принципиально отличается от названных эффектов. От осцилляций Шубникова-де Гааза ВТО отличаются величиной периода (период ВТО в обратном магнитном поле существенно меньше) и температурной зависимостью амплитуды: ВТО наблюдаются как при Т<< , так и в области температур Т , где амплитуда эффекта Шубникова-де Гааза экспоненциально мала – отсюда и название “высокотемпературные” осцилляции (Т – температура, - циклотронная частота, - постоянная Больцмана). Попытка отождествления ВТО с магнетофононным резонансом приводит к граничной энергии оптических фононов, в несколько раз большей своего действительного значения.

В ходе исследований было, в частности, экспериментально изучено влияние на свойства ВТО температуры [5,7], ультраквантовых магнитных полей [4, 17-19, 21], всесторонних и анизотропных деформаций [13, 16], легирования висмута примесями Sb, Te, Sn [7, 8]. Установлено, что период ВТО связан с циклотронной массой носителей заряда и не зависит от энергии ферми [5, 7, 8].

Существуют две альтернативные модели, в которых сделана попытка описать свойства ВТО. Согласно первой из них [10,11] причиной возникновения ВТО являются электрон – дырочные переходы у границ энергетических зон. Возможность таких переходов связана с тем обстоятельством, что в висмуте даже при низких (гелиевых) температурах относительное число занятых состояний носителей заряда над ферми – уровнем, задаваемое выражением

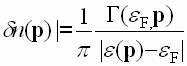|, (1)

достигает 10-2-10-3 (Уширение энергетических уровней обусловлено релаксационными процессами). Уширение уровней в висмуте, соответствующее электрон – примесным, электрон – электронным и электрон – фононным частотам столкновений в гелиевой области температур, составляет (В.С. Винник, И.Я. Коренблит, Е.А. Охрем, А.Г. Самойлович, ЖЭТФ 80, 2031 (1981); R. Hartman, Phys.Rev. 181, 1070 (1969); M.P. Vecchi, J.R. Pereira, M.S. Dresselhaus, Phys.Rev. B14, 298 (1976); В.С. Эдельман, УФН 123, 257 (1977)). Расстояние от края зоны до ферми-уровня . ( Здесь энергия ферми электронов (дырок) в висмуте, импульс носителей заряда, энергия края зоны в и - точках зоны Бриллюэна). Таким образом значение оказывается по порядку величины совпадающим с относительной амплитудой ВТО. Следуя (1), для абсолютной амплитуды ВТО образца размерами 1х1х10 мм получаем: висмут-~ 10-2ом (в соответствии с экспериментом); сурьма-~ 10-6 ом; типичный металл-~ 10-12 ом. Параметр квазиклассичности может уменьшить значение абсолютной амплитуды ВТО в типичном металле еще на 2-3 порядка.

В соответствии с [10,11], при квазиупругом междолинном рассеянии носителей заряда период ВТО в стандартной модели дается соотношением

(2)

где - энергия перекрытия электронной и дырочной зон, - циклотронная масса. При неупругом междолинном рассеянии на акустических фононах с энергией возникает наложение мод с периодами [15]

(3)

С помощью соотношений (2), (3) для висмута получены усредненные значения энергии перекрытия зон мэв и энергии “межзонных” акустических фононов мэв. Первое из этих значений соответствует мэв, что согласуется с наиболее достоверной величиной ферми – энергии электронов, приведенной в цитированном выше обзоре В.С. Эдельмана. Энергия “межзонных” акустических фононов соответствует данным A.A. Lopez, Phys.Rev. 175, 823 (1968). Установлено, что в диапазоне температур 10-70K энергия перекрытия увеличивается примерно на 30% [2,5,7], и это связывается с температурной зависимостью анизотропии решетки.

Оказывается, что ВТО обнаруживают эффект, близкий к удвоению частоты, которое наблюдается в широком интервале направлений магнитного поля H [3]. При этом вторая гармоника по амплитуде соизмерима с первой. Поскольку угловая зависимость периода второй гармоники определяется анизотропией циклотронной массы дырок, ее происхождение связывается с электрон – дырочными переходами вблизи горизонтали, определяемой вершиной валентной зоны в точке зоны Бриллюэна. Структура выражения для соответствующего периода при квазиупругих межзонных переходах совпадает с формулой (2), в которую вместо энергии перекрытия входит сумма . Полученное значение энергетической щели мэв [17] соответствует результатам IR- исследований, и близко к приведенному в обзоре В.С. Эдельмана (см. ссылку выше).

Известно, что циклотронная масса дырок в висмуте не зависит от энергии. Поэтому, комбинируя данные, полученные при измерениях эффекта Шубникова – де Гааза и ВТО, можно получить информацию о ферми – энергии электронов и энергетической щели в точке для полуметаллических сплавов на основе висмута.

В работе [12] предложена альтернативная модель ВТО, согласно которой осцилляции возникают в результате электронно-дырочных переходов между экстремумами подзон Ландау вблизи уровня ферми. При этом циклотронные массы электронов и дырок должны быть кратны. Здесь, как и в [10,11], при некоторых предположениях (см. ниже) период ВТО определяется величиной перекрытия энергетических зон. Казалось бы, экспериментальные результаты полнее описываются в рамках моделей [10,11]. Это прежде всего относится к совместному наблюдению электронных и дырочных периодов ВТО [7,14], реализации ВТО в ультраквантовом пределе [4,18], слабой зависимости относительной амплитуды осцилляций от направления магнитного поля (по этому поводу проводились специальные контрольные измерения). Однако появление теоретических работ, рассматривающих слабозатухающие по температуре осцилляции кинетических коэффициентов в слоистых структурах и тонких пленках (M.V. Kartsovnik et al, Phys. Rev. Lett. 89, 126802 (2002); О.В. Кириченко, И.В. Козлов, ФНТ 28, 509 (2002); И.В. Козлов, ФНТ 29, 1341 (2003)), вновь стимулировало интерпретацию экспериментальных результатов с позиций [12].

В работе [20] была сделана попытка рассчитать и сравнить с измерениями зависимость периода ВТО висмута от направления магнитного поля в трех главных кристаллографических плоскостях (угловые зависимости). В духе модели [12] период ВТО [20]

(4)

связывался с комбинационным сечением

, (5)

равным сумме экстремальных сечений ферми-поверхностей электронов и дырок с целочисленными коэффициентами, относящимися как циклотронные массы дырок и электронов. На первый взгляд создается впечатление об удовлетворительном согласии эксперимента и расчета. Два близких семейства точек на расчетных угловых зависимостях, по мысли автора [20], описывают экспериментально наблюдаемые биения ВТО, а вместо дырочных и электронных осцилляций рассматриваются единые колебания интерференционной природы.

Однако рассмотрение результатов эксперимента в наглядном масштабе [5,7] сразу же демонстрирует издержки подхода [20] – измеренная в бинарной плоскости с весьма малым шагом (1-2 градуса) угловая зависимость периода ВТО совпадает ( с учетом биений) с угловой зависимостью обратных циклотронных масс, в соответствии с [10,11]. Плодотворность идеи о биениях, как следствии электрон – дырочных переходов при испускании и поглощении междолинных акустических фононов [15], демонстрируется определением по экспериментальным данным ВТО характерной фононной энергии, согласующейся с известными из специальных опытов результатами (см. выше), а также аналитическим описанием возрастающего участка температурной зависимости амплитуды ВТО (4-12К) в чистых образцах висмута (данный участок связан с экспоненциальным ростом числа междолинных акустических фононов [15]).

Известно, что введение в висмут примерно одного атомного процента сурьмы приводит (вблизи 4К) к превышению на три порядка частоты междолинных квазиупругих столкновений над частотой междолинных столкновений при рассеянии носителей тока на акустических фононах (ссылки и текст в [15]). Соответственно исчезает нарастание амплитуды ВТО в диапазоне 4-12К, сменяясь затуханием по экспоненциальному закону ( с показателем экспоненты -0.12Т [15]), присущему как висмуту (выше 12К), так и всем исследованным сплавам висмут - сурьма разного состава [7]. Кроме того, при температурах от 4К до 15К ВТО остаются монохроматическими, а биения появляются лишь при дальнейшем увеличении температуры, когда частота междолинных столкновений на акустических фононах сравнивается с частотой междолинных квазиупругих столкновений [15].

По мере легирования висмута сурьмой на угловой зависимости растет относительное число периодов ВТО, связываемых с электронами.

При содержании сурьмы 2.6 ат. процента наблюдаемая в бинарной плоскости угловая зависимость периодов ВТО в целом совпадает с угловой зависимостью обратных циклотронных масс электронов [7].

В соответствии с установленной в чистом висмуте с помощью прецизионных измерений разницей (примерно в 7%) циклотронных масс электронов и дырок (дырочная масса больше) при направлении магнитного поля вдоль тригональной оси (В.С. Эдельман, УФН 123, 257 (1977)), периоды ВТО для данного направления магнитного поля (биссекторная плоскость [14]), идентифицированные как дырочные и электронные, отличаются на 7-9%.

Перечисленная совокупность данных подтверждает связь периода ВТО с циклотронной массой носителей заряда [10], а не с комбинационным сечением [12, 20]. Здесь же уместно отметить формальное сходство моделей [10, 11] и [12, 20]: при равных циклотронных массах электронов и дырок – приближенное равенство реализуется вблизи ориентации Н вдоль тригональной оси – выражение (4) для периода ВТО в квадратичной модели спектра точно совпадает с формулой (2). По этой причине одинаково успешное описание в рамках цитируемых альтернативных моделей [10, 11, 12, 20] влияния внешних воздействий (температуры, деформаций, легирования) на период ВТО не может служить решающим аргументом в пользу какой-либо из рассматриваемых моделей.

Согласно модели [12], ВТО должны исчезать в ультраквантовом пределе по магнитному полю одновременно с осцилляциями Шубникова –де Гааза. Исследования в сильных магнитных полях проводились в работах [4, 17 – 19, 21], и характерные данные сводятся к следующему. Когда поле параллельно бинарной оси , при 15 кэ легкие электроны переходят в ультраквантовый предел (две долины, спиновое расщепление на 10% больше орбитального); при 111 кэ наблюдается последний экстремум ВТО; при 120 кэ дно тяжелых электронов пересекает уровень Ферми [19, 21] (ультраквантовый предел). С другой стороны, при 120 кэ выше уровня Ферми остается несколько (2 - 3 по грубым оценкам с учетом движения ферми - уровня ) дырочных подзон Ландау, т.е. для дырок ультраквантовый предел еще не реализуется. Полученный результат противоречит данным [4, 18], согласно которым в магнитном поле, параллельном биссекторной оси , после перехода всех электронных долин в ультраквантовый предел (12 кэ для самых легких электронов, 25 кэ для более тяжелых, спиновое расщепление на 10% больше орбитального, см. обзор В.С. Эдельмана) ВТО продолжают наблюдаться (эксперименты в цитируемых работах велись до 60 кэ, когда по оценкам выше ферми – уровня остается 5-6 дырочных подзон Ландау). В этой связи отметим, что отсутствие в работе [21], где измерения проводились в полях до 330 кэ, экспериментальных данных в геометрии , так же, как и отсутствие соответствующих комментариев, несколько настораживает.

Далее, когда поле параллельно тригональной оси , ВТО исчезают одновременно с последней дырочной осцилляцией Шубникова-де Гааза вблизи 100 кэ [21] (спиновое расщепление дырок вдвое больше орбитального). При этом, наряду с дном электронной зоны, ниже ферми-уровня остается нулевая подзона Ландау с положительно ориентированными спинами электронов ( спиновое расщепление электронов вдвое меньше орбитального), пересекающая ферми-уровень в существенно больших магнитных полях [22].

Таким образом, в идеологии [12] трудно обобщить наблюдаемые особенности исчезновения ВТО в сильных магнитных полях. Между тем экспериментальные результаты просто понять в рамках модели [10, 11] на основе особенностей зонной структуры висмута. При этом следует учесть, что в магнитном поле, направленном вдоль главных осей, ВТО определяются циклотронными массами дырок (эксперимент).

--> ЧИТАТЬ ПОЛНОСТЬЮ <--