Реферат: О развитии математики в XIX столетии. Гамильтон

jk=i, ki=j, ij=k,

kj=-i, ik=-j, ji=-k

Что же касается остального, то его умножение дистрибутивно, так что

(d+ia+jb+kc)(t+ix+jy+kz)=

=dt-ax-by-cz+i(at+dx+bz-cy)+

+j(bt+dy+cx-az)+k(ct+dz+ay-bx)

Векторы, в частности, перемножаются следующим образом:

(ia+jb+kc)(ix+jy+kz)=

=-(ax+by+cz)+i(bz-cy)+j(cx-az)+k(ay-bx)

Абсолютная, скалярная часть этого кватерниона по терминологии, идущей от Грассмана, называется внутренним произведением двух исходный векторов, а векторная часть - их внешним произведением. Таким образом, внутреннее произведение представляет собой скаляр, а внешнее - вектор.

Я хотел бы сразу же обратить внимание на три важных различия, имеющихся между грассмановым комбинаторным произведением и гамильтоновским подходом:

1. У Грассмана произведение двух единиц eiej не выражается через основные единицы. У Гамильтона же, напротив, эти произведения являются функциями - причем даже линейными - исходных единиц. Величины высших порядков у него не появляются. В результате всего этого постановка вопроса о построении системы высших комплексных чисел становится несколько иной. Вычисления с кватернионами можно мыслить себе с произвольным повторением операций сложения и умножения, что в грассмановой системе не допускается.

2. Грассман с самого начала движим интересом к n-мерному пространству, чего совершенно нет у Гамильтона.

3. У Гамильтона по сравнению с Грассманом есть, однако, одно дополнительное понятие - понятие поля - делающее кватернионы важными с точки зрения физики.

Обе части кватерниона Гамильтон рассматривает как функции точки; он представляет себе, что к каждой точке пространства приложен кватернион, то есть скаляр и вектор. К такому полю кватернионов

t(x,y,z)+iu(x,y,z)+jv(x,y,z)+kw(x,y,z)

он применяет определенные операции, в результате чего возникают новые поля. Операции эти Гамильтон, следуя специальной, разработанной в Кембридже методике, изображает с помощью так называемых "символических обозначений". Скажем, теорему Тейлора в кембриджской школе принято было записывать в виде

где выражение полагалось мыслить расписанным по правилу разложения показательной функции в ряд, а входящие в него произведения означали частные производные .

Применяя этот способ и здесь, Гамильтон строит из частных производных по координатам точки поля так называемые символические "операторы". Важнейшим из них является оператор, обозначенный Гамильтоном знаком и названный им, вследствие сходства с одним древним музыкальным инструментом, "наблой":

Формально с этой наблой обращаются так, как если бы она была вектором. Будучи применена к полю кватернионов, она немедленно приводит к ряду важнейших понятий векторного анализа. Так, например, если t - скаляр, то

является вектором, "градиентом t", указывающим в каждой точке величину и направление наибольшего возрастания t.

Будучи применена к вектору iu+jv+kw, операция дает кватернион

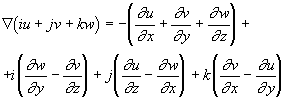
Скалярная часть этого кватерниона называется дивергенцией поля, а векторная - его вихрем.

Попытка разъяснить здесь то исключительное значение, которое понятия эти имеют для физики, завела бы нас слишком далеко. Я укажу лишь, что двукратное применение оператора к скаляру приводит к скаляру