Реферат: Обработка данных в средах MathCAD и LabVIEW

Рис 3б

Построение линейной и кумулятивной гистограмм изображения

Для цифрового изображения формата градации серого, шкала яркостей которого принадлежит целочисленному диапазону 0...255, гистограмма представляет собой таблицу из 256 чисел. Каждое из них показывает количество точек в кадре, имеющих данную яркость.

Линейная гистограмма определяет полный перебор матрицы изображения. Значение элементов матрицы в свою очередь являются индексами массива гистограммы. При выборе какого-либо элемента матрицы к соответствующему элементу массива гистограммы добавляется единица. В итоге, после полного перебора матрицы каждый элемент массива отражает общее число элементов матрицы с соответствующим уровнем яркости (Рис 4а, 5а, Рис п. 5а, б).

У кумулятивной гистограммы любое значение элемента массива равно сумме всех предыдущих (Рис 4б, 5б, Рис п. 6а, б).

MathCAD

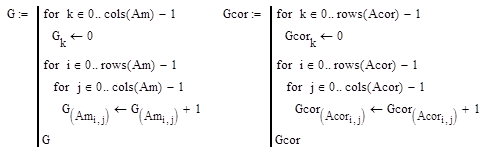
Рис 4а

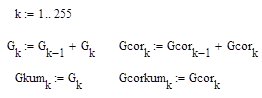
Рис 4б

LabVIEW

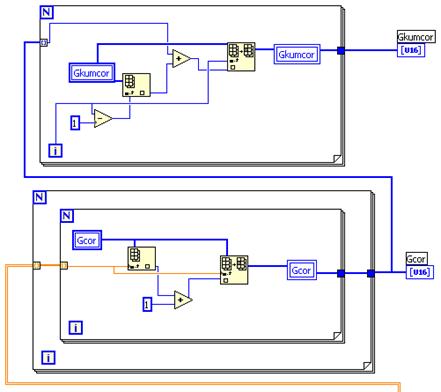
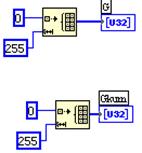
Рис 5а

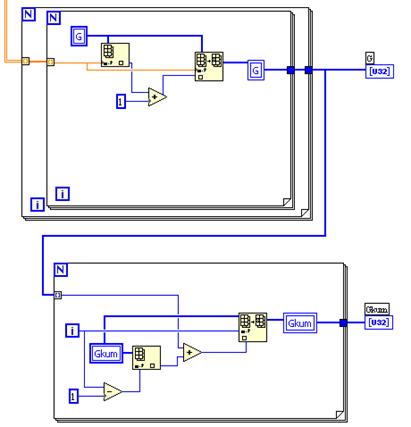
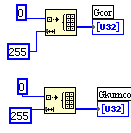
Рис 5б

Бинаризация изображения

Преобразование с пороговой характеристикой превращает полутоновое изображение, содержащее все уровни яркости, в бинарное, точки которого имеют яркости 0 или 255.

Такая операция, называемая иногда бинаризацией или бинарным квантованием, может быть полезной, когда для наблюдателя важны очертания объектов, присутствующих на изображении, а детали, содержащиеся внутри объектов или внутри фона, не представляют интереса (Рис 6а, б).

MathCAD

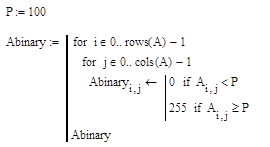
Рис 6а

LabVIEW

Рис 6б

Двукратное увеличение изображений

Масштабирование изображений является весьма важной задачей при анализе изображений. Эта задача неразрывно связанна с проблемой восстановления данных, так как при увеличении физических размеров изображения всегда возникают промежуточные пиксели, значение которых не известно. Определение уровней яркости новых пикселей и есть основная решаемая задача. Однако оба предлагаемых метода хорошо применимы только для одномерных массивов, поэтому сначала необходимо произвести операцию восстановления данных построчно, игнорируя строки только с новыми пикселями (всеми нулевыми значениями), а затем проделать ту же операцию для столбцов полученной матрицы.

Экстраполяция нулевого порядка

Экстраполяция нулевого порядка заключается в приравнивании новому пикселю значения текущего (Рис 7а, б, Рис п. 7).