Реферат: Обработка материалов давлением, определение потерь напора

При движении жидкости в трубопроводе часть энер­гии потока (гидродинамического напора расходу­етсяна преодоление гидравлических сопротивлений.

Последние бывают двух видов:

1) сопротивления по длине , пропорци­ональные длине потока;

2) местные сопротивления , возникнове­ние которых связано с изменением направления или ве­личины скорости в том или ином сечении потока.

К местным сопротивлениям относят внезапное расши­рение потока, внезапное сужение потока, вентиль, кран, диффузор и т. д.

Величина общих потерь энергии (напора) учитыва­ется дополнительным членом , в уравнении Бернулли для реальной жидкости.

Определение величины потерь энергии (напора) при движении жидкости является одной из основных задач гидродинамики.

При движении жидкости в прямой трубе потери энер­гии определяются формулой Дарси — Вейсбаха

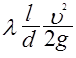= ; (2-27)

где — потери напора по длине, м.

Эту же потерю напора можно выразить в единицах давления:

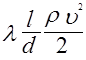(2-28)

где —потери давления, Па; —потери напора,м;—коэффициент сопротивления трения по длине; l- длина трубы, м; d—диаметр трубы, м; v— средняя ско­рость движения жидкости в выходном сечении трубы, м/с: g-ускорение силы тяжести, м/с² ; р—плотность жидкости (газа), кг/м³ .

Коэффициент сопротивления трения по длине

В гидравлических расчетах потерь напора по формуле Дарси — Вейсбаха (2-27) наиболее сложным является определение величины коэффициента сопротивления трения по длине.

Многочисленными опытами установлено, что в общем случае коэффициент сопротивления трения К зависит от числа Рейнольдса и относительной шероховатости стенок канала, т. е. .

Для частных случаев движения жидкости имеем сле­дующие зависимости для определения коэффициента сопротивления трения .

При ламинарном движении коэффициент сопротивле­ния трения не зависит от относительной шероховатости, а является функцией только числа Рейнольдса и опреде­ляется по формуле Пуазейля :

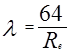; (2-29)

При турбулентном движении в гидравлически глад­ких каналах (трубах) в диапазоне чисел Рейнольдса 15•10³ <<80• 10³ коэффициент сопротивления тре­ния также не зависит от относительной шероховатости стенок и является функцией числа Рейнольдса. Он опре­деляется по формуле Блазиуса :

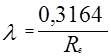(2.30)

В широком диапазоне чисел Рейнольдса для переход­ной области сопротивления коэффициент сопротивле­ния , уже является функцией двух величин: числа Рей­нольдса и относительной шероховатости и может опреде­ляться, например, по формуле Альтшуля:

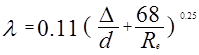(2-30)

Границы этой области сопротивления для круглых труб различной шероховатости определяются следующим неравенством:

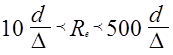. (2-32)

При этом условии ламинарная пленка начинает ча­стично разрушаться, крупные выступы шероховатости уже оголены, а мелкие еще скрыты в толще сохранив­шейся ламинарной пленки.

В квадратичной области сопротивления, когда лами­нарная пленка полностью исчезает и все выступы шеро­ховатости оголены, на величину коэффициента сопротив­ления трения число Рейнольдса уже не оказывает ни­какого влияния, и, как показывает опыт, в этом случаев является функцией только относительной шероховато­сти, т. е.

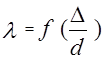; (2-33)

Для определения коэффициента сопротивления в этой области может быть использована формула Б. Л. Шифринсона