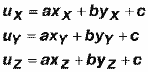Реферат: Один метод построения полигональных изображений

float v2;

float u3;

float v3;

} Triangles[NUM_TRIANGLES];

//Текстура (256 цветов)

unsigned char Texture[TEXTURE_SIZE];

Отдельно требуется указать ракурс, под которым будет видна модель. Наиболее удобным для пользователя было бы задание оси вращения в виде вектора и угла поворота вокруг нее. Однако значительно проще реализовать последовательные повороты по трем углам: вокруг оси X, вокруг оси Y’, в которую перешла ось Y при первом повороте, вокруг оси Z’’, в которую перешла ось Z’ при втором повороте.

Алгоритм построения изображения

Изображение модели строится по отдельным граням, а изображение грани – по отдельным точкам, для каждой из которых определяется цвет. При этом, во-первых, закрашены должны быть все точки внутренней области изображения, во-вторых, цвет точки должен рассчитываться только один раз, что накладывает некоторые ограничения на выбор алгоритма.

Первым этапом построения изображения треугольной грани будет определение координат ее вершин в мировой СК и, в частности, их положения на экране, для чего требуется повернуть СК модели на заранее заданные углы (см. выше). Наиболее изящно такой поворот осуществляется умножением радиуса-вектора вершины на матрицу поворота. Мы же опишем его в терминах обычной координатной геометрии с применением формул поворота «плоской» (!) СК. Пусть x, y, z – начальные, а x’, y’, z’ - конечные координаты вершины, ТАУ – угол поворота, тогда эти формулы приобретают вид:

вокруг оси X:

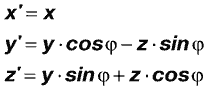
вокруг оси Y:

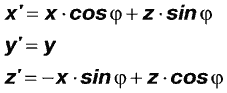
вокруг оси Z:

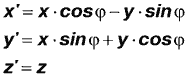
Следует помнить, что наша задача требует осуществлять все три поворота последовательно и при каждом новом повороте использовать в качестве начальных координат те, что получены при предыдущем.

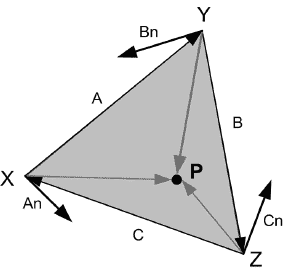
Перейдем ко второму, не менее важному этапу. После того, как контур грани на экране определен, нужно найти все точки (пиксели), лежащие внутри него, иными словами, решить классическую задачу о принадлежности точки внутренней области треугольника. Один из вариантов ее решения (найденный автором статьи) таков. Представим контур грани составленным из векторов, а не отрезков (см. рисунок 1). К каждому из них проведем нормаль. Знаки координат вектора нормали выберем так, чтобы он был направлен в сторону противоположной вершины. Тогда внутри треугольника будут находиться те и только те точки, для которых все три скалярных произведения вектора, проведенного из какой-либо вершины в эту точку, и нормали, проведенной из той же вершины, положительны.

Например, на приведенном рисунке точка P лежит внутри треугольника, поскольку выполняются соотношения (здесь и далее заглавными латинскими буквами будем обозначать точки и векторы, а строчными – координаты):

Для каждой найденной таким образом точки нужно определить ее видимость. Для этого используем широко распространенный метод z-буфера. Буфер представляет собой массив вида

float ZBuffer[SCREEN_WIDTH][SCREEN_HEIGHT];

Каждой точке на экране (пикселю) соответствует один элемент массива, а его значение трактуется как «глубина» этой точки, иными словами, ее координата z в мировой СК. Перед выводом точки ее «глубина» сравнивается с текущим значением в массиве и, если оказывается меньше его, записывается на его место и точка выводится на экран. Таким образом, видимой среди всех точек с одинаковыми координатами x и y оказывается та, у которой координата z минимальна.

Внимательный читатель заметит, что на предыдущем этапе задачу о взаимном расположении точки и треугольника мы решали в плоскости экрана и ни для одной из проверяемых точек координата z вообще неизвестна. Зато известны координаты z вершин треугольной грани, а кроме того, тот очевидный факт, что любая из точек (пусть это будет все та же точка P на рисунке вверху) лежит в плоскости грани. Следовательно, векторы A, C, XP (можно выбрать и другие тройки) компланарны и

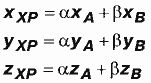
Эта система с неизвестными a, b, Zxp легко решается методом подстановки. Сложив Zx и Zxp, мы получим координату z точки P.

Теперь, если мы убедились, что точка находится внутри треугольника и она не заслонена другими точками, можно приступить к последнему этапу – определению ее цвета исходя из текстурных координат вершин грани, то есть, по сути, отысканию текстурных координат этой точки. При наложении на грань текстура деформируется – растягивается или сжимается – но так, что при этой деформации прямые линии остаются прямыми. Такое преобразование плоскости называется аффинным и задается уравнениями вида

x’ = ax + by + c; y’ = dx + ey + f.

Приведенные уравнения справедливы для координат любой точки, в том числе и для вершин, а значит, если мы, например, хотим найти координату u точки P, то должны сначала определить a, b, c, решив систему уравнений