Реферат: Операции на графах

0

1

1

A₁₂

=

x₂

1

0

1

A₂₁

=

x₂

0

1

1

x₃

0

0

0

x₃

0

0

0

Нетрудно убедиться, что полученным матрицам смежности вершин соответствуют графы G₁ (G₂ ) и G₂ (G₁ ) , представленные на рис. 3.

Декартово произведение графов. Пусть G₁ (X,E₁ ) и G₂ (Y,E₂ ) — два графа. Декартовым произведением G₁ (X,E₁ ) ´ G₂ ( Y ,E₂ ) графов G₁ (X,E₁ ) и G₂ (X,E₂ ) называется граф с множеством вершин X ´ Y , в котором дуга (ребро), идущая из вершины (x_i y_j ) в (x_k y_l ) , существует тогда и только тогда когда существует дуга (x_i x_k ) , принадлежащая множеству дуг E₁ и j = l или когда существует дуга (y_j ,y_l ) , принадлежащая множеству E₂ и i = k .

Выполнение операции декартова произведения рассмотрим на примере графов, изображенных на рис. 4. Множество вершин Z результирующего графа определяется как декартово произведение множеств X ´ Y . Множество Z содержит следующие элементы: z₁ =(x₁ y₁ ), z₂₌ (x₁ y₂ ), z₃ =(x₁ y₃ ), z₄ =(x₂ y₁ ), z₅ =(x₂ y₂ ), z₆ =(x₂ y₃ ) .

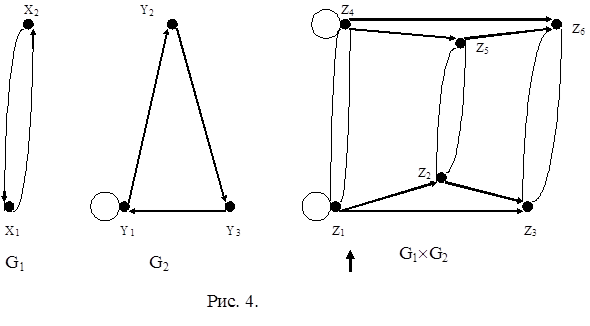Определим множество дуг результирующего графа. Для этого выделим группы вершин множества Z, компоненты которых совпадают. В рассматриваемом примере пять таких групп: две группы с совпадающими компонентами из множества X , и три группы, имеющие совпадающие компоненты из Y . Рассмотрим группу вершин результирующего графа, которые имеют общую компоненту x₁ : z₁ =(x₁ y₁ ), z₂₌ (x₁ y₁ ), z₃ =(x₁ y₃ ). Согласно определению операции декартова произведения графов, множество дуг между этими вершинами определяется связями между вершинами множества Y . Таким образом, дуга (y₁ ,y₁ ) в графе G2 определяет наличие дуги (z₁ ,z₁ ) в результирующем графе. Для удобства рассмотрения всех дуг результирующего графа составим таблицу, в первом столбце которой перечисляются вершины с совпадающими компонентами, во втором – дуги между несовпадающими компонентами, а в третьем и четвертом – дуги в результирующем графе.

№ п.п.	Группы вершин с совпадаю­щими компонентами	Дуги для несовпада­­ю­щих компонент	Дуга ( xi yj ) ® (xk yl )	Дуга ( z a ,z b )
1	z1 =(x1 y1 ), z2= (x1 y2 ), z3 =(x1 y3 )	(y1 ,y1 ) (y1 ,y2 ) (y2 ,y3 ) (y3 ,y1 )	(x1 y1 ) ® (x1 y1 ) (x1 y1 ) ® (x1 y2 ) (x1 y2 ) ® (x1 y3 ) ( x1 y3 ) ® (x1 y1 )	(z1 ,z1 ) (z1 ,z2 ) (z2 ,z3 ) (z3 ,z1 )
2	z4 =(x2 y1 ), z5 =(x2 y2 ), z6 =(x2 y3 )	(y1 ,y1 ) (y1 ,y2 ) (y2 ,y3 ) (y3 ,y1 )	(x2 y1 ) ® (x2 y1 ) (x2 y1 ) ® (x2 y2 ) (x2 y2 ) ® (x2 y3 ) (x2 y3 ) ® (x2 y1 )	(z4 ,z4 ) (z4 ,z5 ) (z5 ,z6 ) (z6 ,z4 )
3	z1 =(x1 y1 ), z4 =(x2 y1 )	(x1 ,x2 ) (x2 ,x1 )	( x1 y1 ) ® (x2 y1 ) ( x2 y1 ) ® (x1 y1 )	(z1 ,z4 ) (z4 ,z1 )
4	z2= (x1 y2 ), z5 =(x2 y2 )	(x1 ,x2 ) (x2 ,x1 )	( x1 y2 ) ® (x2 y2 ) ( x1 y2 ) ® (x1 y2 )	(z2 ,z5 ) (z5 ,z2 )
5	Z3 =(x1 y3 ), z6 =(x2 y3 )	(x1 ,x2 ) (x2 ,x1 )	( x1 y3 ) ® (x2 y3 ) ( x2 y3 ) ® (x1 y3 )	(z3 ,z6 ) (z6 ,z3 )

Граф G₁ ´ G₂ изображен на рис. 4.

Операция декартова произведения обладает следующими свойствами.

1. G₁ ´ G₂ = G₂ ´ G₁