Реферат: Операции на графах
0
1
1
0
x4
0
0
1
0
Полученная матрица смежности вершин A’1 È A’2 соответствует графу G1 È G2 , изображенному на рис.1.
Пересечение графов
Пусть G1 (X1 ,E1 ) и G2 (X2 ,E2 ) – произвольные графы. Пересечением G1 Ç G2 графов G1 и G2 называется граф с множеством вершин X1 Ç X2 с множеством ребер (дуг) E = E1 Ç E2
Операция пересечения обладает следующими свойствами, которые следуют из определения операции и свойств операций на множествах:
G1 Ç G2 = G2 Ç G1 – свойство коммутативности;
G1 Ç (G2 Ç G3) = (G1 Ç G2) Ç G3 – свойство ассоциативности.
Для того чтобы операция пересечения была всеобъемлющей, необходимо ввести понятие пустого графа. Граф G(X,E) называется пустым, если множество X вершин графа является пустым (X= Æ ) . Заметим, что в этом случае и множество E ребер (дуг) графа также пустое множество (E= Æ ) . Пустой граф обозначается символом Æ . Такой граф может быть получен в результате выполнения операции пересечения графов, у которых X 1 Ç X 2 = Æ . В этом случае говорят о непересекающихся графах.
Рассмотрим выполнение операции пересечения графов, изображенных на рис. 2. Для нахождения множества вершин результирующего графа запишем множества вершин исходных графов и выполним над этими множествами операцию пересечения:
X1 = {x1 , x2 , x3 }; X2 = {x1 , x2 , x3 , x4 };
X = X1 Ç X2 = {x1 , x2 , x3 }.
Аналогично определяем множество E дуг результирующего графа:
E1 = {(x1 , x2 ), (x1 , x3 ), (x2 , x1 ), (x2 , x3 ), (x3 , x2 )};
E2 = {(x1 , x3 ), (x2 , x1 ), (x2 , x3 ), (x2 , x4 ), (x3 , x1 )};
E = E1 Ç E2 = {(x1 , x3 ), (x2 , x1 )}.
Графы G1 (X1 ,E1 ) , G2 (X2 ,E2 ) и их пересечение приведены на рис 4.2.
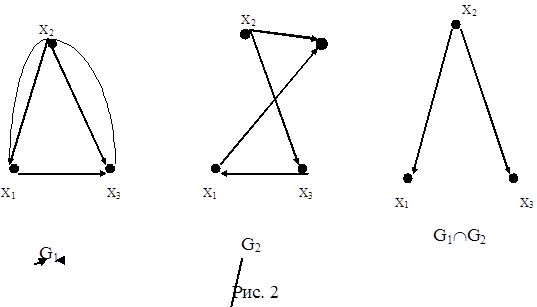
Операция пересечения графов может быть выполнена в матричной форме.