Реферат: Определение законов распределения случайных величин и их числовых характеристик на основе опытны

В итоге получим 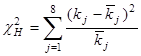= 7,2035

По таблице критических точек распределения ([1], стр. 465), по уровню значимости =0,05 и числу степеней свободы 8-3=5 находим

Т.к. , экспериментальные данные не противоречат гипотезе и о нормальном распределении случайной величины .

Для случайной величины :

Используя предполагаемый закон распределения, вычислим теоретические частоты по формуле

, где - объем выборки, - шаг (разность между двумя соседними вариантами, ,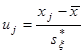

1	7	-1.4036	5.9274	1.1504	0.1941
2	16	-0.7405	12.0665	15.4725	1.2823
3	19	-0.0774	15.8248	10.0820	0.6371
4	6	0.5857	13.3702	54.3197	4.0627
5	6	1.2488	7.2775	1.6319	0.2242
6	5	1.9119	2.5519	5.9932	2.3485
7	1	2.5750	0.5765	0.1794	0.3111

В итоге получим =8.1783

По таблице критических точек распределения ([1], стр. 465), по уровню значимости =0,05 и числу степеней свободы 7 - 3=4 находим

Т.к. , экспериментальные данные не противоречат гипотезе и о нормальном распределении случайной величины .

6. Построить график функции плотности распределения случайной величины в одной системе координат с гистограммой.(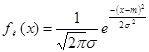 взяв в качестве математического ожидания и дисперсии их статистические оценки и ) и вычислив значение функции в точках: , , а также в точке левее первого и правее правого промежутка группировки.

7. Выполнить задание 6 для случайной величины .

8. Найти доверительные интервалы для математических ожиданий и дисперсий случайных величин и , соответствующие доверительной вероятности .

Найдем доверительный интервал для математического ожидания :

Рассмотрим статистику , имеющую распределение Стъюдента с степенями свободы. Тогда требуемый доверительный интервал определится неравенством . И доверительный интервал для выглядит следующим образом:

Найдем по таблицам ([2], стр. 391). По =0,95 и =120 находим: =1,980. Тогда требуемый доверительный интервал примет вид:

То есть: (20,93721;26,12946).

Найдем доверительный интервал для математического ожидания :

Рассмотрим статистику , имеющую распределение Стъюдента с степенями свободы. Тогда требуемый доверительный интервал определится неравенством . И доверительный интервал для выглядит следующим образом:

Найдем по таблицам ([2], стр. 391). По =0,95 и =60 находим: =2,001. Тогда требуемый доверительный интервал примет вид:

То есть: (20,043;27,056).

Известно, что если математическое ожидание неизвестно, то доверительный интервал для дисперсии при доверительной вероятности имеет вид

Для случайной величины найдем:

.

Таким образом, имеем доверительный интервал: (162,8696; 273,8515).

Для случайной величины найдем

Таким образом, имеем доверительный интервал: (134,82; 277,8554).

(Квантили распределения найдены по таблице [3], стр. 413).

9. Проверить статистическую гипотезу при альтернативной гипотезе на уровне значимости .

Рассмотрим статистику

,

где

,