Реферат: Определитель матрицы

Полученное выражение совпадает с тем, которое было дано в определении, следовательно, для определителя 2-го порядка теорема доказана.

Для произвольного данная теорема доказывается методом математической индукции.

Итак, показано, что определитель может быть разложен по любой строке. Возникает вопрос, а нельзя ли сделать то же самое, использовав произвольный столбец.

Теорема 2. Каков бы ни был номер столбца (), для определителя -го порядка справедлива формула

,

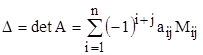называемая разложением этого определителя по -му столбцу .

Докажем теорему для :

.

Данное выражение равно величине определителя, введенной по определению.

Итак, на основании теорем можно сказать, что для вычисления определителя -го порядка необходимо его разложить по произвольной строке или столбцу.

2. Свойства определителей

Рассмотрим ряд свойств, которыми обладают определители.

1. Равноправность строк и столбцов.

Определение 1. Транспонированием определителя называется операция, в результате которой меняются местами строки и столбцы с сохранением порядка их следования .

Определитель, полученный в результате транспонирования, называется транспонированным по отношению к исходному и обозначается .

Свойство 1. При транспонировании величина определителя сохраняется, то есть .

Доказательство этого свойства вытекает из того, что разложение определителя по первой строке тождественно совпадает с разложением по первому столбцу. Данное свойство указывает на равноправность строк и столбцов, поэтому все дальнейшие свойства можно рассматривать лишь для строк.

2. Антисимметрия при перестановке двух строк.

Свойство При перестановке местами двух строк определитель сохраняет свою абсолютную величину, но меняет знак на противоположный .

Докажем для определителя второго порядка. Действительно,

; .

Для определителя -го порядка докажем это свойство по индукции. Пусть свойство справедливо для определителя -го порядка. Разложим определитель -го порядка по любой строке, отличной от переставленных. Тогда переставленные строки входят во все миноры, на которые умножаются элементы , но эти миноры являются определителями -го порядка и меняют свой знак при перестановке строк. Следовательно, и определитель -го порядка также меняет свой знак.

3. Линейное свойство определителя.

Определение Некоторая строка () является линейной комбинацией строк () и () с коэффициентами и , если .

Пользуясь этим определением, перейдем к самому свойству.

Свойство 3. Если в определителе -го порядка некоторая строка () является линейной комбинацией двух строк () и () с коэффициентами и , то , где - определитель, у которого -ая строка равна (), а все остальные - те же, что и у , а - определитель, у которого -ая строка равна (), а все остальные - те же, что и у .

Для доказательства разложим каждый из определителей по -ой строке. Очевидно, что у всех разложений миноры соответствующих элементов будут одинаковы. Вычислим :

Итак, свойство доказано. Очевидно, оно справедливо и для столбцов.

Приведенные три свойства называются основными. Остальные являются их следствиями.

Свойство 4. Умножение всех элементов некоторой строки или столбца определителя на число равносильно умножению определителя на число .