Реферат: Оптимизация химико технологических процессов
Сформулированному обобщенному критерию оптимизации схемы в целом не должны противоречить критерии оптимального функционирования отдельных ее составных частей. Локальные критерии оптимизации должны, с одной стороны, выбираться автономно для данного узла или аппарата, но сдругой стороны не вступать в конфликт с глобальным критерием. Известно, что совокупность оптимальных критериев составных частей общего не обязательно дает совокупный критерий оптимизации целого. Верно и обратное утверждение.
Топологический метод и ХТС
Большая сложность современных ХТС, многомерность их как по числу составляющих элементов, так и по числу выполняемых ими функций, высокая степень взаимосвязанности и параметрического взаимовлияния элементов определяет возникновение при решении задачи анализа и синтеза схем ряда принципиальных трудностей научно-исследовательского, методологического и вычислительного характера. Эти трудности могут быть в некоторой степени преодолены при применении топологического метода анализа ХТС. Этот метод предоставляет возможность формализовать функциональную связь между топологическим представлением системы и количественными характеристиками функционирования системы. С помощью топологического метода анализа можно разрабатывать оптимальную стратегию решения задач анализа функционирования и оптимизации сложных систем.
Применение топологического метода анализа основано на рассмотрении математических топологических моделей систем, которыми являются потоковые и структурные графы. Применение топологических представлений позволяет большой объем существенной информации о сложной ХТС приводить к компактной и наглядной форме. Это уже само по себе дает возможность составить качественное представление о некоторых свойствах исследуемой системы.
Отметим, что с помощью потоковых и структурных графов можно представить физико-химическую структуру исходной смеси, особенности технологической топологии системы в целом и отдельных ее узлов, устанавливать связь между изменениями технологической структуры и количественными характеристиками ХТС.
Основные понятия и определения теории графов
Пусть дано множество Х, которое состоит из элементов, называемых точками. Дан закон, позволяющий установить соотношение Т между каждым элементом множества Х и некоторыми из его подмножеств. Обозначим через Тх некое подмножество множества Х, отвечающее элементу х множества Х. Две математические величины – «множество Х» и «соответствие Т» - определяют граф G, обозначаемый как G = (X, T). Элементы множества Х будем изображать точками, и называть вершинами графа. Соотношения Т будем изображать отрезками (иногда ориентированными), соединяющими элемент с элементами подмножества Тх, и называть ребрами или дугами графа. Граф G называется конечным, если число его вершин конечно. На рис.1,а показан граф, определяемый множеством
X = {x0 , x1 , x2 , x3 , x4, x5 }.

а)
|
|
|
|
|
|

б)
в)
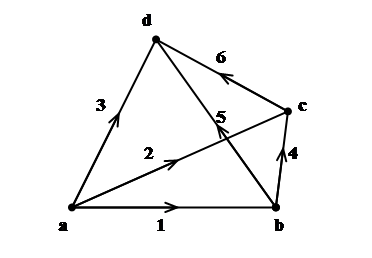
Рис.1. Различные графы: а – граф, определяемый множеством вершин Х = {x0 , x1 , …, x5 }; б – нуль граф; в – граф, определяемый множеством вершин Х = {a, b, c, d}.