Реферат: Оптимизация. Методы многомерного поиска
Задача 1
Найти прямую наилучшим образом аппроксимирующую совокупность экспериментальных точек. Уравнение прямой y=m*x+b. Суммарная ошибка в случае точек определяется выражением SUM=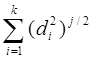
Необходимо найти минимум, SUM, оптимальные значения m,b. Экспериментальные точки заданы.
Задача 2
Емкость бака для жидких отходов должна составитьV л. Изготовляется бак из железобетона толщинойt см. Определить геометрические параметры бака, при которых на его изготовление пойдет минимальное количество бетона.
Задача 3
Емкость бака для жидких отходов должна составитьV л. Изготовляется бак из железобетона толщинойt см. Определить геометрические параметры бака, при которых на его изготовление пойдет минимальное количество бетона, учитывая что бак имеет крышку.
Задача 4
Изготовитель контейнеров проектирует открытый контейнер из листового материала. Заготовка вырезается из листа, сгибается по пунктирным линиям и сваривается четырьмя швами. Каковы должны быть размеры контейнера небольшого объема, если площадь его дна не должна превышать 1 м2 и ни один из линейных размеров a,b,c не должны быть больше другого более чем в 3 раза?
Задача 5
Сравнительно простая с математической точки зрения целевая функция Розенброка y=100 (x2 -x
) 2 + (1+x1 ) 2 описывает поверхность с впадиной.
Минимальное значение целевой функции соответствует точке с координатами M (x,y). Если взять начальную точку во втором квадранте, то не всегда удается обеспечить сходимость. Выбрав исходную точку попытаться решить эту задачу оптимизации:
a) методом покоординатного спуска;
b) градиентным методом.
Литература
1. Шуп Т. “Решение инженерных задач на ЭВМ", 1982
2. Брукс С.Ш." О случайных методах поиска максимума ”, 1958