Реферат: Организация финансов на коммерческих предприятиях. Экономико-статистический анализ производительности труда в хозяйствах центральной зоны Кировской области
3. Определяем величину интервала:
h =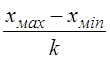 
,
где X max , X min – наибольшее и наименьшее значение группировочного признака, k – количество интервалов
Подставляем значения в формулу и получаем величину интервала равную 2,84 тысячи рублей:
h = 
≈ 3,3 (тыс. руб.)
4. Определяем границы интервалов.
Для этого X min = 2,8 принимаем за нижнюю границу первого интервала, а его верхняя граница равна: X min + h = 2,8+3,3 = 6,1
Верхняя граница первого интервала одновременно является нижней границей второго интервала. Прибавляя к ней величину интервала (h) определяем верхнюю границу второго интервала: 6,1+3,3=9.4
Аналогично определяем границы остальных интервалов.
5. Подсчитаем число единиц в каждом интервале (см. таблицу 1)
Таблица 1
Интервальный ряд распределения хозяйств по выручке на одного работника
| Группы хозяйств по выручке на одного работника | Число хозяйств |
|
2.8-6.1 | 1 |
| 6.1-9.4 | 4 |
| 9.4-12.7 | 10 |
| 12.7-16.0 | 7 |
| 16.0-19.3 | 3 |
| 19.3-22.5 | 3 |
Для наглядности интервальные ряды распределения представленные в таблице 1 можно изобразить в виде гистограммы (см. график 1):
График 1
Распределение хозяйств по выручке на одного работника
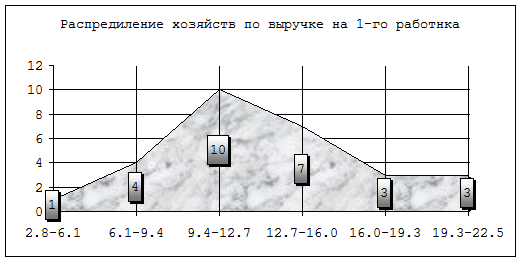
По данным гистограммы можно сделать вывод, что в большинстве хозяйств выручка на одного работника находится в интервале от 9,4 до 12,7 тысяч рублей, а в среднем 11,05 тыс. руб.
Одним из наиболее распространенных законов распределения, с которым сравнивают другие распределения, является нормальное распределение. Для того, чтобы установить верно ли предположение о том, что полученное распределение подчиняется закону нормального распределения, необходимо определить являются ли расхождения между фактическими и теоретическими частотами случайными или закономерными. Для проверки этой статистической гипотезы используeтся критерий, разработанный К. Пирсоном.
Критерий Пирсона определяют по формуле:
Х2 факт. = 
,
где fi и fТ частоты фактического и теоретического распределения.
Теоретические частоты для каждого интервала определяем в следующей последовательности:
1. Для каждого интервала определяем нормированное отклонение (t) по формуле: t = 
где хi – серединное значение интервала;
- средняя величина признака;
- среднее квадратическое отклонение характеризуемого признака в ряду распределения.
Проведем необходимые расчеты параметров исходного ряда распределения:
=
2. Сопоставив с математической таблицей «Значения функции j(t)»
фактические величины t для каждого интервала найдем значение функции нормального распределения.