Реферат: Основы и понятие землеустройства

в) Зональная система плоских прямоугольных координат в проекции Гаусса-Крюгера (Х и Y в метрах):

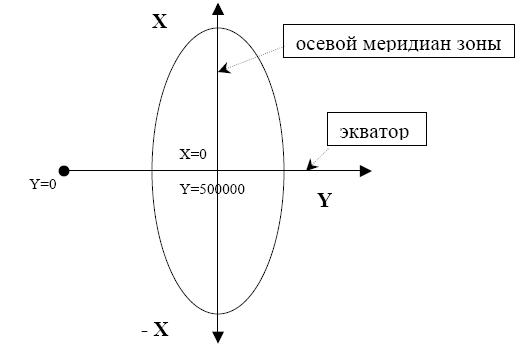
Для однозначного определения местоположения перед ординатой точки записывается номер 6-градусной зоны, например для точки пересечения осей в 12 зоне получим: Y=12500000

г) Система прямоугольных координат Х и Y на плоскости (широко применяется в топографии и прикладной геодезии):

д) Другие системы координат.

2.4. Прямая и обратная геодезические задачи.

Алгоритм решения прямой и обратной геодезической задачи рассмотрим для случая прямоугольной системы координат на плоскости.[4]

В прямой геодезической задаче по известным координатам одной точки (X, Y) дирекционному углу αи длине стороны Dвычисляют координаты другой точки (X, Y).

В обратной геодезической задаче по известным координатам двух точек вычисляют дирекционный угол и длину линии.

Дано: X, Y, X, Y.

Найти: α, D.

Решение:

D = ΔX/cos α = ΔX/cos r = ΔYsin α = ΔYsin r = (ΔX + ΔY),

где ΔX = Х - Х; ΔY = Y - Y.

Для того, чтобы получить значение дирекционного угла, сначала вычисляют значение румба по формуле:

r = arctg (ΔY/ΔX).

Затем по знакам ΔX и ΔY определяют номер четверти и по соответствующей формуле вычисляют значение α:

2.5. Системы высот в геодезии

Высота - расстояние по отвесной линии от уровенной поверхности до точки физической поверхности Земли.

Различают абсолютные высоты , если отсчет ведется от уровенной поверхности Земли (геоида) и относительные , если отсчитываются от произвольной уровенной поверхности.

В России за начало отсчета абсолютных высот принят средний уровень Балтийского моря, отмеченный штрихом на специальной пластине (нуль Кронштадтского футштока).

Геодезические работы по измерению превышений и вычислению высот точек земной поверхности называют нивелированием.

Разность высот двух точек называется превышением: h = H – H.

Превышения с учетом взаимного расположения точек бывают положительные и отрицательные.

Рис. 2. Уровенная и физическая поверхность

Геодезической высотой Нгеод . называется расстояние от эллипсоида до точки на земной поверхности по нормали к эллипсоиду: Нгеод.

Рис. 3. Геодезическая высота