Реферат: Особенности практического применения способов кодирования. Способы декодирования с обнаружением ошибок
Коды Рида-Соломона (РС)
Коды РС являются недвоичными циклическими кодами, символы кодовых слов которых берутся из конечного поля GF(q). Здесь q степень некоторого простого числа, например q=2m .
Допустим, что РС-код построен над GF(8), которое является расширением поля GF(2) по модулю примитивного многочлена f(z)=z3 +z+1. В этом случае символы кодовых слов кода будут иметь значения, представленные в таблице 2.
| Таблица 2 | |||||
| 000 | 0 | 0 | 011 | z+1 | 3 |
| 001 | 1 | 0 | 110 | z2 +z | 4 |
| 010 | z | 1 | 111 | z2 +z+1 | 5 |
| 100 | z2 | 2 | 101 | z2 +1 | 6 |
Кодовые слова РС-кода отображаются в виде многочленов 
,
где N - длина кода; Vi - q-ичные коэффициенты (символы кодовых слов), которые могут принимать любое значение из GF(q).
Эти коэффициенты как это следует из таблицы, также отображаются многочленами с двоичными коэффициентами 
. Коды РС являются максимальными, т.к. при длине кода N и информационной последовательности k они обладают наибольшим кодовым расстоянием d=N-k+1.
Порождающим многочленом g(x) РС-кода является делитель двучлена xN +1 степени меньшей N с коэффициентами из GF(q) при условии, что элементы 
этого поля являются корнями g(x). Здесь 
- примитивный элемент GF(q).
На основе этого определения, а также теоремы Безу, выражение для порождающего многочлена РС-кода будет иметь вид 
.
Степень g(x) равна d-1=N-k=R.
В РС-кодах принадлежность кодовых слов данному коду определяется выполнением d-1 уравнений в соответствии с выражением 
(*), где Vi - символы-коэффициенты из GF(q); z0 , z1 ... zN-1 - ненулевые элементы GF(q).
Элементы z0 , z1 ... zN-1 называются локаторами, т.е. указывающими на номер позиции символа кодового слова.
Например, указателем i - позиции является локатор zi или элемент i GF(q).
Так как все локаторы должны быть различны и причем ненулевыми, то их число в GF(q) равно q-1. Следовательно, такое количество символов должно быть в кодовых словах кода.Поэтому обычно длина РС-кода определяется из выражения N=q-1.
Пример. Допустим, что длина РС-кода равна N, кодовое расстояние d=3, то в соответствии с (*) проверочными уравнениями будут 
Свойства РС-кодов.
1. Циклический сдвиг кодовых слов, символы которых принимают значение из GF(q), порождает новые кодовые слова этого же кода.
2. Сумма по mod2 двух и более кодовых слов дает кодовое слово, принадлежащее этому же коду.
3. Кодовое расстояние РС-кода определяется не по двоичным элементам, а по q-ичным символам.
4. В РС-коде, исправляющем tu ошибок порождающий многочлен определяется из выражения 
. Обычно m0 принимают равным 1. Однако, с помощью разумного выбора значения m0 , иногда можно упростить схему кодера.
5. Корректирующие способности РС-кода определяются его кодовым расстоянием.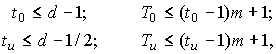 
где T0 и Tu - длина пакетов, в которых обнаруживаются и исправляются ошибки.
Обнаружение ошибок в кодовых словах состоит в проверке условий ((), т.е. определении синдрома 
, элементы которого определяются из выражения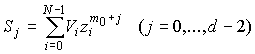 
.
Пример. Требуется сформировать кодовое слово РС-кода над GF(23 ), соответствующее двоичной информационной последовательности a(1,0)=000000011100101.
Так как m=3, то каждый q-ичный символ кода состоит из трех двоичных элементов. Поэтому с учетом таблицы 6 a(x)=3 x2 + 2 x+6 .
Определяем параметры кода. N=q-1=7; k=5; R=2; d=N-k+1=3;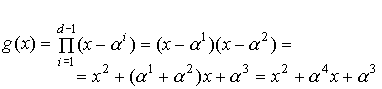 
.
Кодовое слово формируется в соответствии с выражением. 
,
где 
. 
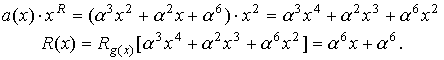
В результате 
или в двоичной форме V(1,0)=000.000.011.100.101.101.101.
ЛИТЕРАТУРА
1. Лидовский В.И. Теория информации. - М., «Высшая школа», 2002г. – 120с.
2. Метрология и радиоизмерения в телекоммуникационных системах. Учебник для ВУЗов. / В.И.Нефедов, В.И.Халкин, Е.В.Федоров и др. – М.: Высшая школа, 2001 г. – 383с.
3. Цапенко М.П. Измерительные информационные системы. - . – М.: Энергоатом издат, 2005. - 440с.