Реферат: Особенности работы в программном пакете MicroCAP-7

Method — выбор метода оптимизации:

Standard Powell — стандартный метод оптимизации Пауэлла,

Stepping Powell — согласно этому методу параметры изменяются от значения Low до значения High с шагом Step. На каждом шаге изменения параметров применяется стандартный метод Пауэлла.

Total Error — корень квадратный из суммарной ошибки (разности между целевой функцией и ее фактической величиной); выводится когда выбрано поле Equates в группе THAT .

Constraints — ограничения типа неравенств и равенств, записываемые на четырех строках, например, PD(R1)<=100m, V(Out)>=1.2, VCE(Q1)*IC(Q1)<=200m

Optimize — начало оптимизации.

Stop — остановка оптимизации.

Apply — изменение на схеме значения параметров в соответствии с результатами оптимизации.

Format — выбор формы представления чисел.

Close — завершение режима оптимизации.

В приведенном примере требуется изменением L1, C1, R1 добиться такого вида АЧХ, чтобы она максимально близко проходила возле 6 заданных точек (частота, амплитуда в дБ): (2e6, 2.188), (4e6, 10.449), (6e6,-1.696), (8e6,-9.103), (10e6, -13.939), (20e6,-27.134). Это означает, что корень квадратный из суммы квадратов отклонений полученной АЧХ от заданных значений в заданных точках принимает минимальное значение. В соответствии с заданной целевой функцией и заполняются поля группы THAT в окне OPTIMIZE (см. рис. 4.18, 4.19). Например Y_Level(DB(V(OUT)),1,1,2e+006) обозначает значение кривой оптимизируемой характеристики (АЧХ в дБ) при значении независимой переменной (частоты) равной 2E6 Hz. Выбор Equates означает, что оптимизация идет для наилучшего удовлетворения условию равества коэффициента передачи в дБ заданному значению 2.188.

Отметим, что в группе THAT вместо Equates может быть выбрано Minimize или Maximize, тогда оптимизация выполняется с целью достижения минимального (максимального) значения кривой Y в выбранной точке X. См. примеры OPT 1… OPT 3 из каталога Analysis\Optimize.

Заполнение полей группы FIND в рассматриваемом примере осуществляется в соответствии с оптимизируемыми параметрами R1, C1, L1 (поля Parameter) и заданными диапазонами их изменения (поля Low и High).

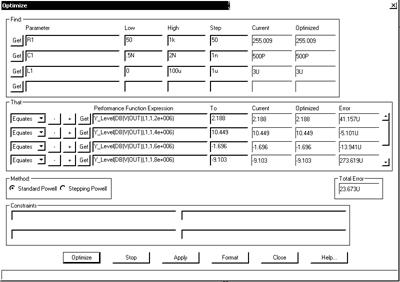
Рис. 4. Вид окна Optimize после проведения оптимизации

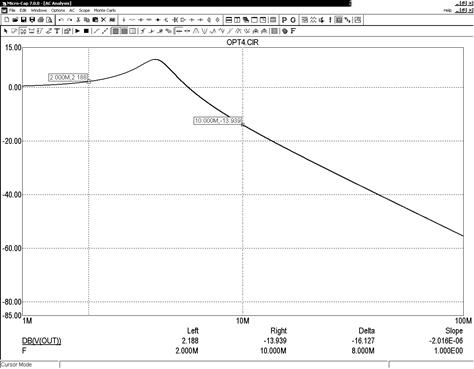
Рис. 5. Вид АЧХ схемы после оптимизации

После заполнения диалогового окна нажатием на панель Optimize выполняют оптимизацию (см. рис. 4) и затем при необходимости нажатием на панель Apply переносят найденные оптимальные значения параметров на схему. Выполняемый после таких действий анализ выведет характеристики схемы при полученных оптимальных значениях параметров (см. рис. 5). По его результатам пользователь может проверить соответствие выполненной оптимизации техническому заданию.

4 Статистический анализ по методу Монте-Карло

При выборе режимов моделирования Transient, AC или DC становится доступен подрежим Monte Carlo для расчета характеристик цепей при случайном разбросе параметров:

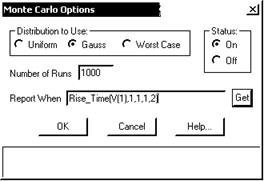
Options — установка параметров метода Монте-Карло (см. рис. 6);

Add Histogram — добавление окна гистограмм (доступно после проведения моделирования);

Delete Histogram — удаление окна гистограмм (доступно после проведения моделирования);

Statistics — статистическая обработка результатов (доступно после построения гистограммы).

В диалоговом окне Monte Carlo Options (рис. 6, а), открываемом по команде Monte Carlo/Options, указывается количество статистических испытаний Number of Runs (не более 30000) и характер закона распределения случайных параметров, заданных значением LOT параметра модели: Uniform равномерное распределение, Gauss — гауссово, Worst Case — наихудший случай. Напомним, что в окне Global Settings задается отношение разброса случайных параметров к среднеквадратическому отклонению SD.

Гауссово распределение (Gauss ) случайной величины x описывается уравнением:

,

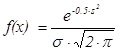Где , m — номинальное значение параметра, s — величина отклонения, указываемая после ключевого слова LOT (здесь абсолютное значение), x — значение случайной величины, f ( x ) — плотность вероятности принятия случайной величиной значения x.

Равномерное распределение (Uniform ) — означает одинаковую вероятность принятия случайной величиной x любого значения внутри диапазона, определяемого параметром модели LOT.

а)