Реферат: Параметричний резонанс

Розглянемо рух математичного маятника, точка підвісу якого z₀ коливається вертикально з частотою со і амплітудою а:z₀ = = acost. Внаслідок коливань точки підвісу система координат, початок якої збігається з точкою підвісу, неінерціальна. Тому, слід врахувати силу інерції, яка в розглядуваному випадку дорівнює

l_z = — m₀ = m² a cos t.

Потенціал цієї сили виражається формулою

U = —l_z z = —mla² cos cos,

де 8 — кут відхилення маятника від вертикалі, вибраний за уза­гальнену координату. Функція Лагранжа в цьому разі має вигляд

L = + mgl cos + mla ² cos t cos ,

а рівняння Лагранжа

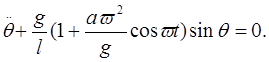
Для малих коливань ( 1) це рівняння зводиться до лінійного рівняння

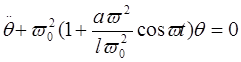
де = g/l.

Таким чином, коливання точки підвісу математичного маятника еквівалентне зміні з часом його параметрів:

Параметром, що залежить від часу, тут є частота

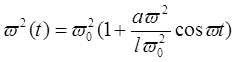
Ця залежність за певних умов, як буде показано нижче, приводить до наростання з часом амплітуди коливань, тобто до параметрич­ного резонансу або параметричної нестійкості.

Розглянемо спочатку загальний випадок, коли функція (t) в рівнянні (40.1) є довільною періодичною функцією часу

(t + Т) = (t)

з періодом Т — 2/. У зв'язку з цим можна сказати, що рівнян­ня (40.1) інваріантне відносно перетворення t→t+T. Звідси випливає, що коли (t) є розв'язком рівняння то функція (t— Т) теж має бути його розв'язком. З курсу диференціальних рівнянь відомо, що рівняння другого порядку завжди має два лі­нійно незалежні розв'язки Ql (t) і 92 (t), а будь-який інший розв'я­зок можна подати у вигляді лінійної комбінації цих двох розв'яз­ків. Зокрема,

₁ (t + T)= а_{11 1} (t) + а_{12 2} (t),

₂ (t + T) = а_{21 1} (t) + a_{22 2} (t).

Завжди можна вибрати систему лінійно незалежних розв'язків так, щоб вони були дійсними. Оскільки аргумент t функцій ₁ (t + T) і ₂ (t + T) дійсний, то ₁ (t + T) і ₂ (t + T) також будуть дійсними. Звідси випливає, що коефіцієнти а₁₁ в формулах дійсні; крім того, їхній визначник відмінний від нуля, інакше функції ₁ (t + T) і ₂ (t + T) були б лінійно залежними. Справді, якщо припустити, що визначник

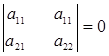
то а₁₁ =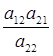, а

₁ (t + T) = 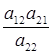₁ (t) + а_{12 2} (t + T) =[a_{21 1} (t)+a_{22 2} (t)] = ₂ (t + T)

що означає лінійну залежність функцій ₁ (t + T) і ₂ (t + T)/ Покажемо, що завжди можна вибрати два таких лінійно неза­лежних розв'язки рівняння, що зміна їх при заміні tна t+ Т зводиться до множення на деякий сталий .множник, тобто (t + T) = . Справді, нехай ₁ (t) і ₂ (t) не мають такої властивості. Тоді помножимо першу рівність на деяку величину , а другу — на і додамо їх:

^’ (t + T)

Підберемо числа і так, щоб виконувалися різності

Це система однорідних рівнянь відносно величин і , розв'я­зок якої існує, якщо

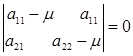
Звідси знаходимо два, взагалі кажучи, комплексно спряжених зна­чення величини : ₁ і ₂ , кожному з яких відповідає оди:І розв'я­зок системи однорідних рівнянь. Поклавши в = ₁ , знаходимо Тоді із співвідношення

₁ ^’ (t + T)

Аналогічно для = ₂ , маємо

₂ ^’ (t + T)

Отже, завжди можна вибрати два таких лінійно незалежних розв'язки рівняння, щоб зміна їх при заміні tна t+ Т зво­дилась до множення на сталий множник:

₁ ^’ (t + T), ₂ ^’ (t + T)

Такі ж співвідношення справедливі для похідних за часом

₁ ^’ (t + T), ₂ ^’ (t + T)

Формули можна записати тотожно так:

;

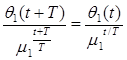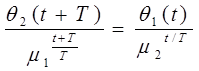
Звідси випливає, що функції

П₁ (t) = ; П₂ (t) =

є періодичними з періодом Т. Отже, система лінійно незалежних розв'язків рівняння має вигляд

₁ (t + T), ₂ ^’ (t + T),

Сталі ₁ і ₂ , зв'язані між собою співвідношенням, яке можна вивести так. Помножимо рівняння, які задовольняють функції ₁ і ₂ ,

;

відповідно на ₁ і ₂ і віднімемо від першого друге. В результаті дістанемо

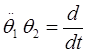
звідки випливає, що вираз l(t) = = constне залежить від часу. Тому l(t+ Т) = l(t). Оскільки з одного боку l (t + T) = ₁ (t +T) ₂ (t + T) = _{1 2} l(t), а з іншого — l (t+ T) = = l (t), то

_{1 2} =1

Оскільки коефіцієнти визначника а_{і j} дійсні, то величини ₁ і ₂ , або дійсні, або комплексно-спряжені. Тоді, враховуючи співвід­ношення, покладемо ₁ = е^zT , ₂ = е^{- zT} де z — комплексна число, яке можна знайти, розв'язавши рівняння.

Таким чином, використовуючи співвідношення, робимо висновок, що два лінійно незалежних розв'язки рівняння з періодичним коефіцієнтом (t) = (t + T) можна записати-у вигляді (теорема Флоке):

₁ (t + T), ₂ ^’ (t + T),

--> ЧИТАТЬ ПОЛНОСТЬЮ <--