Реферат: Перпендикулярность геометрических элементов

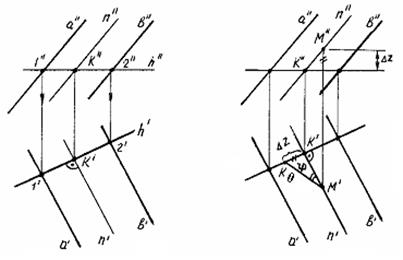
Рис. 67

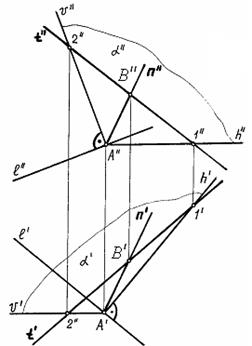
Угол наклона прямой n к плоскости H определяется как угол между прямой и ее проекцией на плоскость H. Строим KK ¢^H (рис. 69). Тогда угол j — искомый угол наклона прямой n к плоскости H.

На рис. 68 построена линия наибольшего наклона плоскости  к горизонтальной плоскости проекций — прямая n . Угол наклона плоскости  к плоскости H получают при определении натуральной величины отрезка KM при построении прямоугольного треугольника по проекциям K ¢M ' и .

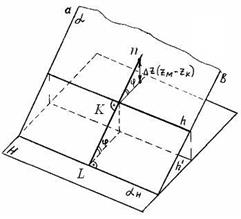
Рис. 69

3 Прямая, перпендикулярная к плоскости

Прямая, перпендикулярная к плоскости, если перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости. На основании теоремы о проецировании прямого угла в качестве прямых плоскости общего положения удобнее всего использовать ее линии уровня.

Поэтому, проводя перпендикуляр к плоскости, необходимо брать в этой плоскости две такие прямые: горизонталь и фронталь.

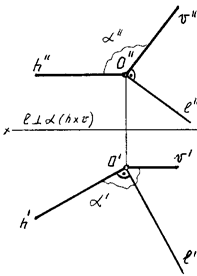
Проекции прямой, перпендикулярной к плоскости, на комплексном чертеже перпендикулярны к соответствующим проекциям ее линий уровня, т.е. если прямая линия перпендикулярна плоскости, то ее горизонтальная проекция должна быть перпендикулярна горизонтальной проекции горизонтали, а ее фронтальная проекция — фронтальной проекции фронтали (рис. 70) или соответствующим следам плоскости (рис. 71).

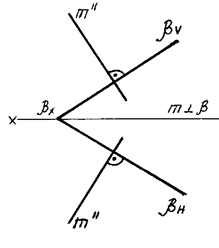Рис. 70	Рис. 71

На рис. 72 изображена плоскость общего положения  (a ||b ), к которой к которой требуется провести перпендикулярную прямую.

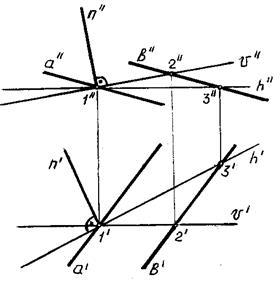
Рис. 72

Проводим в данной плоскости горизонталь h (через точки 1,3) и фронталь v (через точки 1,4) (рис. 72).

Затем из точки 1 проводим прямую n перпендикулярно к горизонтали и фронтали плоскости следующим образом:

n ¢^h ¢; n ²^h ².

Построенная прямая n (n' , n'' ) является искомым перпендикуляром к плоскости .

4. Перпендикулярные плоскости

Две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную данной плоскости. Построение таких плоскостей может быть выполнено двумя путями:

1) плоскость проводится через перпендикуляр к другой;

2) плоскость проводится перпендикулярно прямой, принадлежащей другой плоскости.

На рис. 73 изображены прямая общего положения и плоскость общего положения  (а ´b ). Требуется построить через прямую плоскость, перпендикулярную к плоскости .

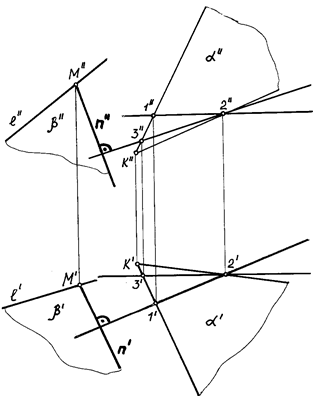
Рис. 73

Для решения задачи необходимо через какую-нибудь точку данной прямой, например, точку М, провести перпендикуляр к плоскости , заданной пересекающимися прямыми a и b.

Проводим в плоскости  горизонталь h и фронталь v (рис. 73).

Далее из точки М , взятой на прямой , опускаем перпендикуляр n , пользуясь рассмотренным выше положением: n' ^h' ; n'' ^v'' , т.е. горизонтальная проекция перпендикуляра будет перпендикулярна горизонтальной проекции горизонтали, а фронтальная его проекция — перпендикулярна фронтальной проекции фронтали (рис. 73).

Плоскость  (Çn ), проходящая через прямую n , будет перпендикулярна к плоскости .

6.5 Перпендикулярные прямые

Две прямые перпендикулярны в том и только в том случае, если через каждую из них можно провести плоскость, перпендикулярную к другой прямой.

На рис. 74 изображена прямая общего положения, к которой требуется провести перпендикулярную прямую.