Реферат: Перпендикулярность геометрических элементов
План
1. Теорема о проецировании прямого угла
2. Главные линии плоскости
3. Прямая, перпендикулярная к плоскости
4. Перпендикулярные плоскости
5. Перпендикулярные прямые
1. Теорема о проецировании прямого угла
Возможны три случая проецирования прямого угла:
1. Если обе стороны прямого угла прямые общего положения, то прямой угол проецируется искаженно на все три плоскости проекций.
2. Если обе стороны прямого угла параллельны какой-либо плоскости проекций, то прямой угол проецируется на эту плоскость в натуральную величину.
3. Если одна сторона прямого угла параллельна какой-либо плоскости проекций, то прямой угол проецируется на эту плоскость в натуральную величину, рис. 64. Это основная теорема о проецировании прямого угла.
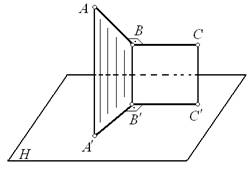
Рис. 64
Дано: ÐАВС = 90°; ВСúú Н. Необходимо доказать: ÐА ¢В ¢С ¢ = 90°.
1. ВС ^АВВ ¢А ¢
ВС ^АВ , следовательно ВС ^ВВ ¢ - по свойству ортогонального проецирования
2. В ¢С ¢úúВС
3. В ¢С ¢^АВВ ¢А ¢
4. В ¢С ¢^А ¢В ¢ - что и требовалось доказать
2. Главные линии плоскости
Линии уровня плоскости
Кроме прямых линий общего положения, в плоскости отмечают три главные линии: горизонтальную (горизонталь), фронтальную (фронталь) и линию наибольшего наклона. Эти линии применяют как вспомогательные: они упрощают решение задач. Две из них — горизонтальная и фронтальная — уже рассматривались.
Необходимо добавить, что все горизонтальные линии плоскости параллельны между собой, а их горизонтальные проекции параллельны горизонтальному следу плоскости (рис. 65). Горизонтальный след плоскости — одна из горизонталей.
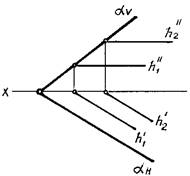 |  |
| Рис. 64 | Рис. 65 |
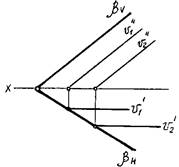
Все фронтальные линии плоскости параллельны между собой, а их фронтальные проекции параллельны фронтальному следу плоскости. Фронтальный след плоскости — одна из фронтальных линий (рис. 66).
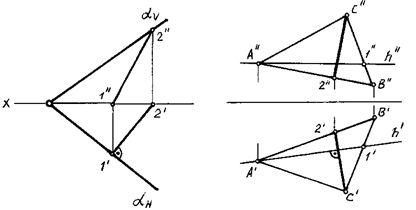
Рис. 66
Линии наибольшего наклона плоскости
Прямые плоскости, перпендикулярные к прямым уровня этой плоскости, называются линией наибольшего наклона (ЛНН) данной плоскости к соответствующей плоскости проекций.
Линии наибольшего наклона плоскости перпендикулярны к ее следам или к линиям уровня (либо к ее горизонталям, либо к фронталям, либо к ее профильным прямым) (рис. 67).
В случае перпендикулярности к горизонтали определяется наклон к плоскости проекций H (при этом ЛНН называют линией наибольшего ската ), перпендикулярности к фронтали — наклон к плоскости проекций V, перпендикулярности к профильной прямой — наклон к плоскости проекций W.
На рис. 67, 68 дано изображение плоскости (а ||b ), для которой требуется построить линию наибольшего наклона к горизонтальной плоскости проекций H.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--