Реферат: Пьезоэлектрики и их свойства

Легко видеть, что необходимость су­ществования обратного пьезоэффекта сле­дует из закона сохранения энергии и факта существования прямого эффекта. Рассмотрим пьезоэлектрическую пластин­ку (рис. 5) и предположим, что мы сжима­ем ее внешними силами F. Если бы пьезо­эффекта не было, то работа внешних сил равнялась бы потенциальной энергии упруго деформированной пластинки. При наличии пьезоэффекта на пластинке появляются заряды и возникает электрическое поле, которое заключает в себе дополнительную энергию. По закону сохранения энергии отсюда следует, что при сжатии пьезоэлектрической пластинки совершается большая работа, а значит, в ней возникают дополнительные силы F1, противодействующие сжатию. Это и есть силы обратного пьезоэффекта. Из приведенных рассуждений вытекает связь между знаками обоих эффектов. Если в обоих случаях знаки зарядов на гранях одинаковы, то знаки деформаций различны. Если при сжатии пла­стинки на гранях появляются заряды, указанные на рис. 5, то при создании такой же поляризации внешним полем пластинка будет растягиваться.

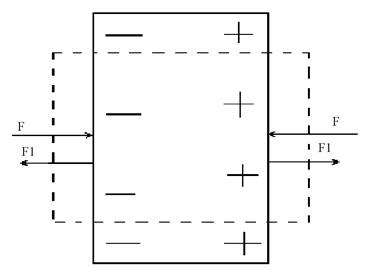Рис .5. Связь прямого и обратного пьезоэлектрических эффектов.

Обратный пьезоэлектрический эффект имеет внешнее сходство с электрострикцией. Однако оба эти явления различны. Пьезоэффект зависит от направления поля и при изменении направ­ления последнего на противоположное изменяет знак. Электрострикция же не зависит от направления поля. Пьезоэффект наблю­дается только в некоторых кристаллах, не обладающих центром симметрии. Электрострикция имеет место во всех диэлектриках как твердых, так и жидких.

Если пластинка закреплена и деформироваться не может, то при создании электрического поля в ней появится дополнительное механическое напряжение Его величина s пропорциональна напряженности электрического поля внутри кристалла:

s=-bЕ (4)

где b - тот же пьезоэлектрический модуль, что и в случае прямого пьезоэффекта. Минус в этой формуле отражает указанное выше соотношение знаков прямого и обратного пьезоэффектов.

Полное механическое напряжение внутри кристалла складывается из напря­жения, вызванного деформацией, и напряжения, возникшего под влиянием элек­трического поля. Оно равно

s=Cu-bE (5)

Здесь С есть модуль упругости при деформации одностороннего растяжения (мо­дуль Юнга) при постоянном электрическом поле. Формулы (51.2) и (52.2) являют­ся основными соотношениями в теории пьезоэлектричества.

При написании формул мы выбирали u и Е в качестве незави­симых переменных и считали D и s их функциями. Это, конечно, необязательно, и мы могли бы считать независимыми переменными другую пару величин, одна из которых — механическая, а другая — электрическая. Тогда мы получили бы тоже два линейных соотношения между u, s, Е и D, но с другими коэффициентами. В за­висимости от типа рассматриваемых задач удобны различные формы записи основ­ных пьезоэлектрических соотношений.

Так как все пьезоэлектрические кристаллы анизотропны, то постоянные e, С и b зависят от ориентации граней пластинки относительно осей кристалла. Кроме того, они зависят от того, закреплены боковые грани пластинки или свободны (за­висят от граничных условий при деформации). Чтобы дать представление о поряд­ке величины этих постоянных мы приведем их значения для кварца в случае, ког­да пластинка вырезана перпендикулярно оси Х и ее боковые грани свободны:

e=4,5; С=7,8 10¹⁰ Н/м² ; b=0,18 Кл/м² .

Рассмотрим теперь пример применения основных соотношений (4) и (5) Положим, что кварцевая пластинка, вырезанная, как указано выше, растягивает­ся вдоль оси X, причем обкладки, касающиеся граней, разомкнуты. Так как заряд обкладок до деформации был равен нулю, а кварц является диэлектриком, то и после деформации обкладки будут незаряженными. Согласно определению элек­трического смещения это значит, что D=0. Тогда из соотношения (4) следует, что при деформации внутри пластинки появится электрическое поле c напряженностью

E=-(b/e0e)u (6)

Подставляя это выражение в формулу (5), находим для

механического на­пряжения в пластинке

s=Cu-b(-(b/e0e)u)=C(1+(b² /e0eC))u (7)

Напряжение, как и в отсутствие пьезоэлектрического эффекта, пропорционально деформации. Однако упругие свойства пластинки теперь характеризуются эффек­тивным модулем упругости

С' == С (1 + b² /e0eС). (8)

который больше С. Увеличение упругой жесткости вызвано появлением добавоч­ного напряжения при обратном пьезоэффекте, препятствующего деформации. Влияние пьезоэлектрических свойств кристалла на его механические свойства характеризуется величиной

К²⁼ b² /e0eC (9)

Квадратный корень из этой величины (К) называется константой электромехани­ческой связи Пользуясь приведенными выше значениями e, С и b, находим, что для кварца К² ~0.01 Для всех других известных пьезоэлектрических кристаллов К² оказывает также малым по сравнению с единицей и не превышает 0,1.

Оценим теперь величину пьезоэлектрического поля. Положим, что к граням кварцевой пластинки, перпендикулярным к оси X, приложено механическое на­пряжение 1 105⁵ Н/м² . Тогда, согласно (7), деформация будет равна u=1,3 10^{- 6} . Подставляя это значение в формулу (6), получаем |E|==5900 В/м=59 В/см. При толщине пластинки, скажем, d==0,5 см напряжение между обкладками будет равно U=Еd~30 В. Мы видим, что пьезоэлектрические поля и напряжения могут быть весьма значительными. Применяя вместо кварца более сильные пьезоэлектрики и используя должным образом выбранные типы деформации, можно полу­чать пьезоэлектрические напряжения, измеряемые многими тысячами вольт.

Пьезоэлектрический эффект (прямой и обратный) широко при­меняется для устройства различных электромеханических преоб­разователей. Для этого иногда используют составные пьезоэлементы, предназначенные для осуществления деформаций разного типа.

На рис.6 показан двойной пьезоэлемент (составленный из двух пластинок), работающий на сжатие. Пластинки вырезаны из крис­талла таким образом, что они одновременно либо сжимаются, либо растягиваются. Если, наоборот, сжимать или растягивать такой пьезоэлемент внешними силами, то между его обкладками появ­ляется напряжение. Соединение пластинок в этом пьезоэлементе соответствует параллельному соединению конденсаторов.

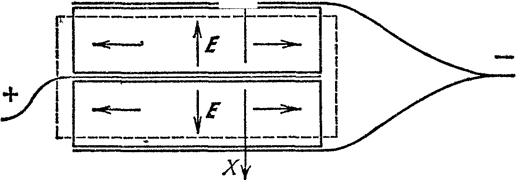
Рис. 6. Двойной пьезоэлемент, работающий на сжатие.

3. Диэлектрики

На рис. 7 показан пьезоэлемент работающий на изгиб. При появ­лении напряжения на обкладках одна из пластинок сжимается в попе­речном направлении и удлиняется в продольном, а другая - растяги­вается и укорачивается, отчего и возникает деформация изги­ба. Если изгибать такой пьезо­элемент внешними силами, то между его обкладками возни­кает электрическое напряже­ние. Соединение пластинок в этом случае соответствует по­следовательному соединению конденсаторов. Очевидно, что такой пьезоэлемент не отвеча­ет на сжатия и растяжения: в этом случае в каждой из пла­стинок возникает электрическое поле, но поля направлены противо­положно, и поэтому напряжение между обкладками равно нулю. Электромеханические преобразователи находят многочисленные применения в разнообразной электроакустической и измерительной аппаратуре. Укажем на пьезоэлектрические микрофон и телефон, пьезоэлектрический адаптер (в электрических проигрывателях пате­фонных пластинок), манометры, измерители, вибраций и др. Осо­бенно важные применения имеют пьезоэлектрические колебания кварца. Если поместить кварцевую пластинку между пластинами конденсатора и создать между пластинами переменное напряжение, то при частоте электрических колебаний, совпадающей с одной из собственных механических частот пластинки, наступает механи­ческий резонанс и в пластинке возникают очень сильные механиче­ские колебания. Такая кварцевая пластинка является мощным излучателем волн сверхзвуковой частоты (кварцевые излучатели), используемых в технике, биологии и медицине, а также в многочис­ленных физических и физико-химических исследованиях. Пьезо­электрические колебания применяются также для стабилизации частоты генераторов электрических колебаний в радиотехнике и в других технических устройствах.

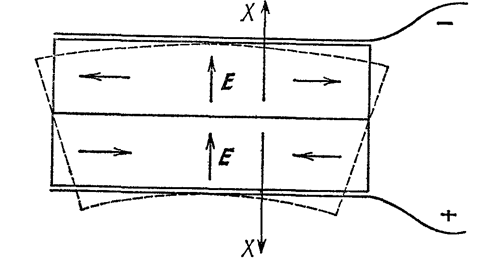
Рис .7. Двойной пьезоэлемент, тающий на изгиб.

4. СПИСОК ЛИТЕРАТУРЫ.

1) “Электричество” С.Г. Калашников, Москва, 1977г.

2) “Электротехнические материалы” Ю.В. Корицкий, Москва, 1968г.

3) “Радиопередающие устройства” Г.А. Зейтленка, Мо­сква, 1969г.