82,05·650·(0,2920-0,0967·0,378)/31 = 439 см³ /моль.

Результаты расчета плотности приведены в табл.6.6 и на рис. 6.9. Для 298 К имеем:

= 298/650 = 0,458;

= 0,29607 – 0,09045·0,458 –0,04842·0,458² = 0,244;

= 0,33593–0,33953·0,458+1,51941·0,458² +1,11422·0,458⁴ = 0,354;

= 0,354·(1–0,378·0,244)·439 = 140,9 см³ /моль;

= 134,222/140,9 = 0,952 г/см³ .

Метод Йена и Вудса

Метод предназначен для прогнозирования плотностей жидкостей при любых давлениях. В приложении к плотности насыщенной жидкости метод заключается в следующем. Приведенная плотность жидкости, находящейся на линии насыщения, коррелирована с приведенной температурой:

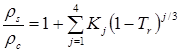,(6.21)

где - мольная плотность насыщенной жидкости, - критическая плотность вещества, - приведенная температура.

Коэффициенты являются функциями критического коэффициента сжимаемости и вычисляются по уравнениям

;(6.22)

при ;(6.23)

при ;(6.24)

;(6.25)

.(6.26)

Пример 6.5

Методом Йена и Вудса рассчитать плотность жидкого изобутилбензола, находящегося на линии насыщения в диапазоне 298-650 К. Критический коэффициент сжимаемости изобутилбензола равен 0,28, критический объем составляет 480 см³ /моль.

Решение

1. Вычисляем значения коэффициентов K_j :

;

;

;

.

2. Критическая плотность изобутилбензола:

г/см³ .

3. Рассчитываем плотность жидкого изобутилбензола, находящегося на линии насыщения. Для 298 К имеем

=0,8056 г/см³ .

Фрагмент результатов расчета при других температурах приведен в табл. 6.6., на рис. 6.9. дается сопоставление их с полученными методом Ганна-Ямады и другими методами.

Метод Чью-Праусница