Реферат: Поиск оптимальных решений

– квадратичная форма с матрицей Гессе,

.

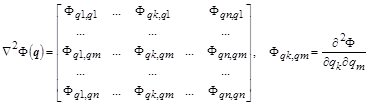Условием достижения локального минимума является положительная определенность квадратичной формы с матрицей Гессе в точке остановки, в которой . Квадратичная форма положительна тогда и только тогда, когда все главные миноры ее квадратной матрицы, например, матрицы A , положительны:

.

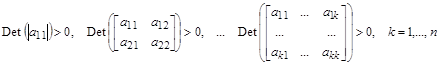Из проведенных рассмотрений можно сделать заключение, что для линейных функционалов любая остановка итерационного процесса соответствует локальному экстремуму, так как производные выше второй равны нулю.

3 . Функционал для градиентного равенства

Функционалом можно считать любую функцию, минимум которой необходимо определить. Вся сложность задачи заключается в ограничениях, накладываемых на переменные и их взаимосвязь. Если ограничения отсутствуют, то говорят о задаче безусловной оптимизации (Пример МНК). К последней сводится и система нелинейных алгебраических уравнений, заданных в неявной форме:

если из системы сконструировать квадратичный функционал такого вида

,

где – масштабирующие (весовые) коэффициенты.

Подстановка функционала в покомпонентную систему градиентных уравнений приводит к итерационной процедуре с вычислением на каждом шаге следующих выражений:

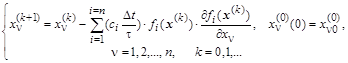
Если система уравнений линейная, то частные производные будут константами . Вместе с = они определяют индивидуальный весовой коэффициент каждого уравнения исходной линейной системы в формулах градиентной итерационной процедуры.

Для нелинейной системы, функционал которой в окрестности точки минимума можно аппроксимировать квадратичной функцией с положительно определенной матрицей Гессе, в итерационном выражении

и после приравнивания оставшихся слагаемых нулю и сокращения суммы на вектор несложно получить соотношение

,

которое приводит к итерационной формуле

идентичной формуле Ньютона в применении к решению системы нелинейных уравнений

.

Для строго выпуклой, квадратичной функции решение получается за одну итерацию. Этот момент особенно привлекателен для задач линейного программирования, когда целевая функция линейная или квадратичная, а ограничения представлены системой линейных равенств и неравенств. При этом системы равенств и неравенств вводят в общий функционал в виде суммы квадратов функций невязок (аддитивно).

4. Функционалы в задачах условной оптимизации

Конструирование выпуклого квадратичного функционала с учетом ограничений рассмотрим для следующей задачи:

В приведенную обобщенную запись задачи минимизации включены:

Минимизируемая функция вектора искомых параметров (функция цели или критериальная функция):

f (x ), .