Реферат: Показатели качества и эффективности управленческих решений
α1,н 1 =0,37/(0,37+0,29+0,26)=0,4
α2,н 1 =0,29/(0,37+0,29+0,26)=0,32
α3,н 1 =0,26/(0,37+0,29+0,26)=0.28
3. Определение усреднённых по оценкам всех экспертов относительных важностей всех путей на всех уровнях дерева целей:
,
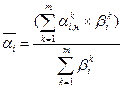где 
- усреднённая оценка относительной важности i-го пути;
- компетентность к-го эксперта в i-м пути.
Пример расчёта усреднённых по оценкам всех экспертов относительных важностей всех путей на всех уровнях дерева целей:
_
α1 =(0,4*1+0,43*1+0,36*0,8)/(1+1+0,8)=0,4
4. Установление наиболее предпочтительных путей движения к главной цели на каждом уровне:
I уровень – путь 1 (0,4);
II уровень – путь 3.1 (0,7)
III уровень – пути 1.1.1 и 3.1.1 (0,71)
Таблица 2.4 - Расчёт относительной важности путей дерева целей
| Уровень | Номера путей | Эксперт №1 | Эксперт №2 | Эксперт №3 | _ α | ||||||
| α | αн | β | α | αн | β | α | αн | β | |||
| 1 | 1 | 0,37 | 0,40 | 1 | 0,31 | 0,43 | 1 | 0,23 | 0,36 | 0,8 | 0,40 |
| 2 | 0,29 | 0,32 | 1 | 0,22 | 0,31 | 1 | 0,28 | 0,43 | 0,9 | 0,35 | |
| 3 | 0,26 | 0,28 | 1 | 0,19 | 0,26 | 1 | 0,13 | 0,2 | 0,8 | 0,25 | |
| 2 | 1.1 | 0,27 | 0,73 | 1 | 0,21 | 0,68 | 1 | 0,19 | 0,66 | 0,8 | 0,69 |
| 1.2 | 0,1 | 0,27 | 1 | 0,1 | 0,32 | 1 | 0,1 | 0,34 | 0,8 | 0,31 | |
| 2.1 | 0,19 | 0,66 | 1 | 0,19 | 0,66 | 1 | 0,24 | 0,71 | 0,8 | 0,67 | |
| 2.2 | 0,1 | 0,34 | 1 | 0,1 | 0,34 | 0,8 | 0,1 | 0,29 | 1 | 0,32 | |
| 3.1 | 0,24 | 0,71 | 1 | 0,23 | 0,69 | 0,8 | 0,23 | 0,69 | 1 | 0,70 | |
| 3.2 | 0,1 | 0,29 | 1 | 0,1 | 0,31 | 0,9 | 0,1 | 0,31 | 1 | 0,30 | |
| 3 | 1.1.1 | 0,24 | 0,71 | 1 | 0,3 | 0,75 | 1 | 0,19 | 0,66 | 1 | 0,71 |
| 1.1.2 | 0,1 | 0,29 | 1 | 0,1 | 0,25 | 1 | 0,1 | 0,34 | 0,8 | 0,29 | |
| 1.2.1 | 0,23 | 0,69 | 1 | 0,19 | 0,64 | 1 | 0,23 | 0,69 | 0,8 | 0,67 | |
| 1.2.2 | 0,1 | 0,31 | 1 | 0,1 | 0,36 | 1 | 0,1 | 0,31 | 0,8 | 0,33 | |
| 2.1.1 | 0,19 | 0,66 | 1 | 0,17 | 0,63 | 1 | 0,17 | 0,63 | 0,8 | 0,64 | |
| 2.1.2 | 0,1 | 0,34 | 1 | 0,1 | 0,37 | 1 | 0,1 | 0,37 | 0,8 | 0,36 | |
| 2.2.1 | 0,17 | 0,63 | 1 | 0,18 | 0,64 | 0,9 | 0,27 | 0,73 | 1 | 0,67 | |
| 2.2.2 | 0,1 | 0,37 | 1 | 0,1 | 0,36 | 0,9 | 0,1 | 0,27 | 0,9 | 0,33 | |
| 3.1.1 | 0,3 | 0,75 | 1 | 0,24 | 0,71 | 0,8 | 0,19 | 0,66 | 1 | 0,71 | |
| 3.1.2 | 0,1 | 0,25 | 1 | 0,1 | 0,29 | 0,8 | 0,1 | 0,34 | 1 | 0,29 | |
| 3.2.1 | 0,27 | 0,43 | 1 | 0,31 | 0,43 | 0,8 | 0,31 | 0,43 | 1 | 0,43 | |
| 3.2.2 | 0,19 | 0,31 | 1 | 0,22 | 0,31 | 0,8 | 0,22 | 0,31 | 1 | 0,31 | |
| 3.2.3 | 0,16 | 0,26 | 1 | 0,19 | 0,26 | 0,8 | 0,19 | 0,26 | 1 | 0,26 | |
Для того, чтобы выбрать наиболее обоснованные варианты возможных управленческих решений, устанавливается относительная предпочтительность движения к главной цели.
Выбор возможных решений осуществляется в следующей последовательности:
1. Определение относительной предпочтительности движения к цели:
,
где: Р – относительная предпочтительность движения к цели взаимосвязанных путей в дереве целей;
- усреднённые нормированные относительные важности взаимосвязанных путей в дереве целей при движении по наиболее предпочтительному пути уровня от низшего уровня к высшему (i=1,f);
f - общее число уровней в дереве решений.
Для наиболее предпочтительного пути 3-го уровня цепочки путей:
3.1.1 – 3.1 – 3: Р=0,71*0,7*0,25=0,124
1.1.1 – 1.1 – 1: Р=0,71*0,69*0,4=0,196
Для наиболее предпочтительного пути 2-го уровня цепочки путей:
3.1.2 – 3.1 – 3: Р=0,29*0,7*0,25=0,051
3.2.1 – 3.1 – 3: Р=0,43*0,7*0,25=0,075
3.2.2 – 3.1 – 3: Р=0,31*0,7*0,25=0,054