Реферат: Полярные диаграммы и энергетические уровни волновых функций жесткого ротатора
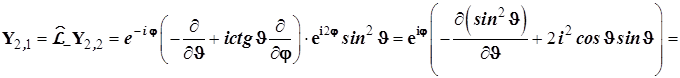
![]() (4.121)
(4.121)
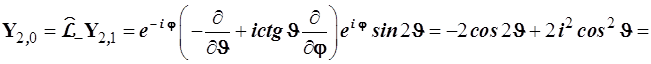
![]() (4.122)
(4.122)
Отсюда получаются d-функции
![]() ;
;![]()
![]() .
.
Величины ![]() ;
;![]() ;
;![]() представлены в таблице 4.6.
представлены в таблице 4.6.
4.3.8.11. Аналогично получается весь набор f-функций
![]()
![]()
![]()
![]() (4.123)
(4.123)
Все найденные s-, р-, d- и f-орбитали сведём в таблицу 4.6.
Таблица 4.6.
Сферические волновые функции![]()
| Уровень | l | m | Символ Y | ||||
| s | 0 | 0 | 1 | 1 | |||
| p | 1 | – “ – | |||||
| 0 | 1 | – “ – | |||||
| d | 2 | – “ – | |||||
| – “ – | |||||||
| 0 | 1 | – “ – | |||||
| f | 3 | – “ – | |||||
| – “ – | |||||||
| – “ – | |||||||
| 0 | 1 | – “ – |
Полярные диаграммы волновых функций жесткого ротатора.
4.3.9.1 В разделе 3.2.7. были рассмотрены полярные диаграммы волновых функций плоского ротатора. Они же – графические образа функции сомножителя ![]() Теперь проанализируем полярные диаграммы функции
Теперь проанализируем полярные диаграммы функции ![]() для чего будем откладывать на радиус-векторе, исходящем из центра под углом
для чего будем откладывать на радиус-векторе, исходящем из центра под углом ![]() к оси z, значения функции
к оси z, значения функции ![]() (рис.4.6.).
(рис.4.6.).
4.3.9.2. В таблице 4.6 суммированы орбитали жесткого ротатора ![]() с комплексными сомножителями
с комплексными сомножителями ![]() которые являются собственными функциями операторов полной энергии, квадрата момента импульса и его проекции на ось z. Однако, графический образ комплексных функций недоступен. На рис. 4.7. представлены полярные диаграммы действительных функций
которые являются собственными функциями операторов полной энергии, квадрата момента импульса и его проекции на ось z. Однако, графический образ комплексных функций недоступен. На рис. 4.7. представлены полярные диаграммы действительных функций ![]() , получаемых как линейные комбинации
, получаемых как линейные комбинации ![]() аналогично построенным в разделе 3.2.6 функциям плоского ротатора. При этом, для состояний, описываемых такими действительными функциями
аналогично построенным в разделе 3.2.6 функциям плоского ротатора. При этом, для состояний, описываемых такими действительными функциями ![]() утрачивается определенность в значении проекции момента импульса
утрачивается определенность в значении проекции момента импульса ![]() , но сохраняется постоянное значение энергии и модуля момента импульса. Как видно на рис. 4.6 и 4.7, число узловых плоскостей на полярных диаграммах равно квантовому числу l . Анализ знаков волновых функций указывает, что орбитали s- и d- являются четными, а p- и f- нечётными по отношению к операции инверсии.
, но сохраняется постоянное значение энергии и модуля момента импульса. Как видно на рис. 4.6 и 4.7, число узловых плоскостей на полярных диаграммах равно квантовому числу l . Анализ знаков волновых функций указывает, что орбитали s- и d- являются четными, а p- и f- нечётными по отношению к операции инверсии.