Реферат: Полные лекции по аэродинамике и динамике полета. Часть 1
а дивергенция скорости :
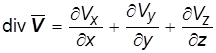. (1.7)
Циркуляцией скорости по замкнутому контуру L с определенным направлением обхода называется криволинейный интеграл:
. (1.8)
Известные теоремы векторных полей [4] применимы и к полю скоростей. Теорема Стокса :
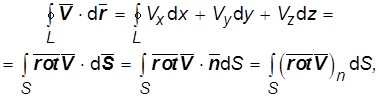(1.9)
справедлива при ориентации обхода контура L и нормали к натянутой на него поверхности 
по правилу правого винта, а теорема Остроградского-Гаусса :
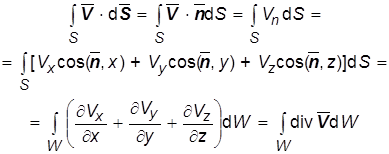(1.10)
при условии, что замкнутая поверхность ограничивает объем W .
Полную производную по времени от скаляра A (
,t ) можно определить по известной [4] формуле:
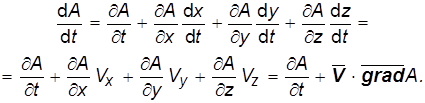(1.11)
Производную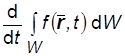 
от интеграла по произвольному подвижному объему W , где от t зависит не только подынтегральная функция, но и объем, вычислим с помощью определения производной:
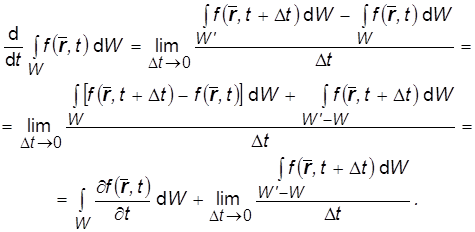
В последнем пределе W' – W образуется сдвигом элементарных площадок dS поверхности S , ограничивающей W , на расстояние Vn dS . Кроме того, при Dt ® 0: f (
,t +Dt ) ® f (
,t ) и деформированная поверхность S ¢ ® S , поэтому предел принимает значение 
(сравните с (1.4)) или 
по теореме Остроградского-Гаусса (1.10). Откуда в силу уравнения (1.11):
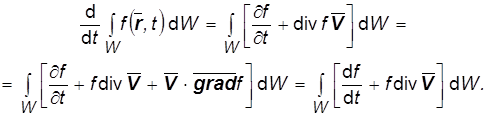(1.12)
Вектор 
¹ 0 тоже можно рассматривать, как поле вектора ротора скорости (,t ) – вихревое поле . Непосредственной проверкой легко убедиться, что всегда div = 0. Отсюда по теореме Остроградского-Гаусса следует, что поток ротора скорости сквозь любую замкнутую поверхность равен нулю:
. (1.13)
В вихревом поле по аналогии с полем скоростей выделяют вихревую линию :
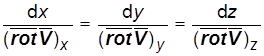(1.14)
и вихревую трубку . Так как через боковую поверхность вихревой трубки по определению нет потока ротора скорости, то из (1.13) вытекает постоянство такого потока через любое ее поперечное сечение (первая кинематическая теорема Гельмгольца о вихрях ). Эта величина называется интенсивностью вихревой трубки . Согласно теореме Стокса (1.9) она равна циркуляции скорости по контуру, образующему вихревую трубку:
. (1.15)
1.3. Уравнение неразрывности
Как известно, плотность вещества в физике вводится предельным переходом: 
, где в механике сплошной среды следует понимать под Dm массу вещества, заключенную в объеме DW. Посмотрим, как будет выглядеть закон сохранения массы 
для произвольного подвижного объема сплошной среды, для которого 
. Из (1.12) тогда следует:
,
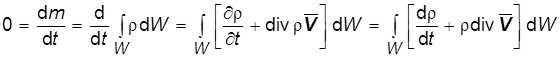или в силу произвольности объема W :
. (1.16)
Это уравнение носит название уравнения неразрывности (непрерывности) .
Рассмотрим частные случаи уравнения неразрывности. Для стационарного (установившегося) движения сплошной среды из (1.16) с учетом (1.7) следует:
, (1.17)
а если, кроме того, среда несжимаемая (
, в том числе и неоднородная), то:
. (1.18)
Т.е. по теореме Остроградского-Гаусса (1.10) установившийся поток скорости несжимаемой среды (1.4) сквозь любую замкнутую поверхность равен нулю. Так как через боковую поверхность трубки тока по определению нет потока скорости, то поток через любое ее поперечное сечение одинаков:
(1.19)
и численно равен объемному расходу сплошной среды. Отсюда можно сделать вывод: внутри объема несжимаемой сплошной среды трубки тока (а также линии тока) не могут ни начинаться, ни заканчиваться .
1.4. Безвихревое и вихревое движение
Движение сплошной среды в некоторой области называется безвихревым , если в ней 
= 0, и вихревым , если ¹ 0 хотя бы в части этой области, называемой вихрем .
| |
Из определения 
(1.6) следует, что вихревое движение характеризуется наличием вращения каждой частицы . Этот факт иллюстрируется рис. 1, на котором крайние точки бесконечно малой частицы среды имеют разные скорости в силу наличия ненулевой величины 
. Если центр этой частицы покоится, а все другие частные производные скорости равны нулю, то очевидно, что 
¹ 0 характеризует именно вращение бесконечно малой частицы среды. В безвихревом движении такого вращения нет и каждая частица среды совершает лишь поступательное движение. Вообще говоря, вихревое движение возникает в реальной природе, благодаря наличию границ (свободной поверхности, твердых стенок или твердых тел), а также явлению вязкости.
Примерами безвихревого движения могут служить:
— состояние покоя среды,