Реферат: Понятие экономического роста и факторы его определяющие

Равновесие является устойчивым, поскольку независимо от исходного значения к экономика будет стремиться к равновесному состоянию, т.е. к k*. Если начальное k1 ниже k*, то валовые инвестиции (sƒ(k) будут больше выбытия (dk) и запас капитала будет возрастать на величину чистых инвестиций. Если k2>k*, это означает, что инвестиции меньше, чем износ, а значит запас капитала будет сокращаться, приближаясь к уровню k* (см. рис. 2).

Норма накопления (сбережения) непосредственно влияет на устойчивый уровень фондовооруженности. Рост нормы сбережения с s1 до s2 сдвигает кривую инвестиций вверх из положения s1ƒ(k) до s2(k) (см. рис. 3).

Рис.3

В исходном состоянии экономика имела устойчивый запас катала k1*, при котором инвестиции равнялись выбытию. После повышения нормы сбережения инвестиции выросли на(i′1-i1) , а запас капитала (k1*) и выбытие (dk1) остались прежними. В этих условиях инвестиции начинают превышать выбытие, что вызывает рост запаса капитала до уровня нового равновесия k2*, которое характеризуется более высокими знаниями фондовооруженности и производительности труда (выпуск на одного занятого, у).

Таким образом, чем выше норма сбережения (накопления), тем более высокий уровень выпуска и запаса капитала может быть достигнут в состоянии устойчивого равновесия. Однако повышение нормы накопления ведёт к ускорению экономического роста в краткосрочном периоде, до тех пор, пока экономика не достигнет точки нового устойчивого равновесия.

Очевидно, что ни сам процесс накопления, ни увеличение нормы сбережения не могут объяснить механизм непрерывного экономического роста. Они показывают лишь переход от одного состояния равновесия к другому.

Для дальнейшего развития модели Солоу поочередно снимаются две предпосылки: неизменность численности населения и его занятой части (их динамика предполагается одинаковой) и отсутствие технического прогресса.

Предположим, население растёт с постоянным темпом n. Это новый фактор, влияющий вместе с инвестициями и выбытием на фондовооруженность. Теперь уравнение, показывающее изменение запаса капитала на одного работника, будет выглядеть как: ∆k=i-dk-nk или ∆k=i-(d+n)k.

Рост населения аналогично выбытию снижает фондовооруженность, хотя и по-другому - не через уменьшение наличного запаса капитала, а путем распределения его между возросшим числом занятых. В данных условиях необходим такой объем инвестиций, который не только бы покрыл выбытие капитала, но и позволил бы обеспечить капиталом новых рабочих в прежнем объёме. Произведение nk показывает, сколько требуется дополнительного капитала в расчете на одного занятого, чтобы капиталовооруженность новых рабочих была на том же уровне, что и старых.

Рис. 4 Рис. 5

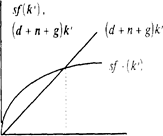
k k′* k′

(капитал на эффективную единицу труда)

Условие устойчивого равновесия в экономике при неизменной фондовооруженности k* можно будет записать теперь так:

∆k=sƒ(k)-(d+n)k=0 или sƒ(k)=(d+n)k

Данное состояние характеризуется полной занятостью ресурсов (рис.4).

В устойчивом состоянии экономики капитал и выпуск на одного занятого, т.е. фондовооруженность (k) и производительность (у) труда остаются неизменными. Но, чтобы фондовооруженность оставалась постоянной и при росте населения, капитал должен возрастать с тем же темпом, что и население, т.е.:

∆Y/Y=∆L/L=∆K/K=n.

Таким образом, рост населения становится одной из причин непрерывного экономического роста в условиях равновесия.

Отметим, что с увеличением темпа роста населения возрастает угловой коэффициент кривой (d+n)k , что приводит к уменьшению равновесного уровня фондовооруженности (k′*), следовательно, к падению у.

Учет в модели Солоу технологического прогресса видоизменяет исходную производственную функцию. Предполагается трудосберегающая форма технологического прогресса, Производственная функция будет представлена как Y=F(K,LE), где E- эффективность труда, а LE- численность условных единиц труда с постоянной эффективностью Е. Чем выше Е, тем больше продукции может быть произведено данным числом работников. Предлагается, что технологический прогресс осуществляется путем роста эффективности труда Е с постоянным темпом g. Рост эффективности труда в данном случае аналогичен по результатам росту численности занятых: если технологический прогресс имеет темп g=2%, то, например, 100 рабочих могут произвести столько же продукции, сколько ранее производили 102 рабочих. Если теперь численность занятых (L) растет с темпом n, а Е растет с темпом g, то (LЕ) будет увеличиваться с темпом (n+g).

Включение технологического прогресса несколько меняет и анализ состояния устойчивого равновесия, хотя ход рассуждений сохраняется. Если определить k' как количество капитала в расчете на единицу труда с постоянной эффективностью, т.е. k'=K/LE, а y'=Y/LE, то результаты роста эффективных единиц труда аналогичны росту численности занятых (увеличение количества единиц труда с постоянной эффективностью снижает величину капитала, приходящегося на одну такую единицу). В состоянии устойчивого равновесия (рис. 5) уровень фондовооруженности k'* уравновешивает, с одной стороны, влияние инвестиций, повышающих фондовооруженность, а, с другой стороны, воздействие выбытия, роста числа занятых и технологического прогресса, снижающих уровень капитала в расчете на эффективную единицу труда: sƒ(k′)=(d+n+g)k′.

В устойчивом состоянии (k′*) при наличии технологического прогресса общий объём капитала (К) и выпуска (У), будут расти с темпом (n+g). Но в отличие от случая роста населения, теперь будут расти с темпом g фондовооруженность (K/L) и выпуск (Y/L) в расчете на одного занятого; последнее может служить основой для повышения благосостояния населения. Технологический прогресс в модели Солоу является, следовательно, единственным условием непрерывного роста уровня жизни, поскольку лишь при его наличии наблюдается устойчивый рост выпуска на душу населения (у).

Характеристика основных переменных модели Солоу в состоянии устойчивого равновесия

При отсутствии роста населения и технологического прогресса		При росте населения с темпом n		При росте населения с темпом n и технологическом прогрессе с темпом g
Переменная	Темп роста	Переменная	Темп роста	Переменная	Темп роста
L	0	L	n	L	N
LE	n+g
K	0	K	n	K	n+g
k′=K/LE	0
k=K/L	0	k=K/L	0	k=K/L	G
Y	0	Y	n	Y	n+g
y′=Y/LE	0
y=Y/L	0	y=Y/L	0	y=Y/L	g

Таким образом в модели Солоу найдено объяснение механизма непрерывного экономического роста в режиме равновесия при полной занятости ресурсов.

Как известно, в кейнсианских моделях норма сбережения задавалась экзогенно и определяла величину равновесного темпа роста дохода. В неоклассической модели Солоу при любой норме сбережения рыночная экономика стремится к соответствующему устойчивому уровню фондовооруженности (k*) и сбалансированному росту, когда доход и капитал растут с темпом (n+g). Величина нормы сбережения (накопления) является объектом экономической политики и важна при оценке различных программ экономического роста.

Поскольку равновесный экономический рост совместим с различными нормами сбережения (как мы видели, увеличение s лишь на короткое время ускоряло рост экономики, в длительном периоде экономика возвращалась к устойчивому равновесию и постоянному темпу роста в зависимости от значения n и g), возникает проблема выбора оптимальной нормы сбережения.