Реферат: Понятие
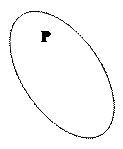
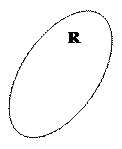
Таким образом, равнообъёмные понятия - это, по существу, разные наборы понятиеобразующих признаков, отнесённые к одному классу. Иначе говоря, это одно и то же множество объектов, мыслимое через разные понятиеобразующие признаки. Равнообъёмность понятий P и Q может быть записана в виде формулы P =Q . Равнообъёмные понятия заслуживают особого внимания именно потому, что они представляют в создании один и тот же логический класс. Способность сознания отражать объекты в нескольких понятиях, обладающих разнящимся содержанием, имеет огромное познавательное значение. Она позволяет изучать некоторый фрагмент действительности с различных точек зрения, выделяя смысловые единицы с несовпадающими наборами понятиеобразующих признаков. Особый интерес представляют ситуации, в которых равнообъёмность понятий первоначально не была известна и обнаружилась лишь в ходе познания, какого-то фрагмента деятельности. Такие равнообъёмные понятия - это своеобразный анахронизм, след некогда существовавших иллюзорных представлений. Долгое время два разных положения Венеры на небесном своде, наблюдаемых в утреннее и вечернее время суток, ошибочно связывали с существованием двух различных небесных тел. это заблуждение сначала (у древних греков) выразилось в понятиях «Фосфор» и «Геспер», а позднее закрепилось в понятиях «Утренняя звезда» и «Вечерняя звезда», которые, естественно, использовались в те времена как разнообъёмные. Отнесение их к одной планете (то есть установление равнообъёмности) явилось существенным астрономическим открытием.
Перекрещивание.
Понятия P и Q находятся в отношении перекрещивания , если имеются три класса: а) объекты, общие для объёмов P и Q , б) объекты, входящие в объём P , но не входящие в объём Q , в) объекты, входящие в объём Q , но не входящие в объём P (Рис.2). В отношении перекрещивания находится, например, такие понятия: «журналист» и «офицер», «роман» и «сатирическое произведение», «город на
|

 ??????? ? ???????? ??????????? ??û. ?????? ???????? ??????????? ????? ?), ??????? ?? ? ?????????? ????? ???????? ???????? ??????????? ???????. ? ??????????? ???????? ???????? ??????????? ? ?????? ???? ??????? ????? ?????????????? ????????? ???????????-???????? ? ????????? ???????????? ???????.
??????? ? ???????? ??????????? ??û. ?????? ???????? ??????????? ????? ?), ??????? ?? ? ?????????? ????? ???????? ???????? ??????????? ???????. ? ??????????? ???????? ???????? ??????????? ? ?????? ???? ??????? ????? ?????????????? ????????? ???????????-???????? ? ????????? ???????????? ???????.
Третий пример примечателен тем, что область пересечения понятий охватывает лишь один предмет. Таким образом, в отношении перекрещивания могут находиться понятия, объёмы которых имеют хотя бы один общий объект. Область пересечения интересна тем, что с её помощью достаточно строго и одновременно кратко характеризуются и другие виды отношений. Область пересечения рассмотренных выше равнообъёмных понятий равна объёму каждого из них в отдельности.
Легко убедиться в том, что единичные понятия не могут находиться в отношении перекрещивания (поэтому на графических схемах они иногда изображаются как точки, а не окружности).
Внеположенность.
|

 ??????? P ? Q ?????????? внеположенными , ???? ?? ?????? ????????? ????????? ???? ????? (???.3). ????? ??????? ?????: ?????? ????????????? ??????? ?? ???????? ?? ?????? ?????? ???????, ?????????????, ??????? ?? ??????????? ???????? ?????? ?????. ??????: ?????? ? ????????, ?????????? ? ???????? ????????, ??????????? ??????? ? ????????????? ???????. ?????? ??????? ???????????? ??? ??????? ??????
??????? P ? Q ?????????? внеположенными , ???? ?? ?????? ????????? ????????? ???? ????? (???.3). ????? ??????? ?????: ?????? ????????????? ??????? ?? ???????? ?? ?????? ?????? ???????, ?????????????, ??????? ?? ??????????? ???????? ?????? ?????. ??????: ?????? ? ????????, ?????????? ? ???????? ????????, ??????????? ??????? ? ????????????? ???????. ?????? ??????? ???????????? ??? ??????? ??????
внеположенности -контрарность и контрадикторность . Этими отношениями связаны такие понятия, в содержании которых мыслятся взаимоисключающие, противоположные признаки. Степень противоположности признаков может быть различной.
Контрарными (противными) называются понятия, содержащие предельно противоположные признаки, выделенные на какой-то шкале оценок. Посредством контрарных понятий фиксируются два класса, занимающих крайние позиции в некоем упорядоченном множестве свойств, действий, состояний. Например: «старость - молодость», «горячий - холодный», «богач - бедняк». Контрадикторными (противоречащими) два понятия называются тогда, когда в содержании одного из них подвергаются отрицанию признаки, мыслимые в содержании второго. Поскольку при этом не выделяются некоторые полярные классы объектов, контрадикторность иногда характеризуют как ослабленную (в сравнении с контрарностью) противоположность. Таковы, например, пары понятий: «старость - не старость», «горячий - не горячий», «богач - не богач». Уже из приведенных примеров ясно, чем различаются контрарность и контрадикторность. Еще отчетливее это различие демонстрируется при помощи графических схем. Сумма объемов контрарных понятий (рис.4) не исчерпывает некоего универсального класса, поскольку имеется, по крайней мере, одно состояние или свойство, занимающее среднюю позицию между ними (применительно к приведенным примерам: «не-молодость и не старость, а средний возраст», «не горячий, но и не холодный, а теплый или прохладный», и т. п.).
|


 ??? ??????????????? ??????? ??? ??????? ????????? ??? ???????? ?????????, ????? ?? ??????? ????????? ???????????? ????????????? ????? (???.5). ? ????? ????, ?????????, ??????? ??? ????????? ????????? ?? ???? ???????? ?????, ????? ???????? (?? ?????? ? ?????????, ?? ? ? ???????? ????????). ??????? ????????? ????????? - ?? ????????? (? ??????? ?? ????????? ????????? - ??????????) ??????????? ??? ?????????? ?????????. ????? ?? ????
??? ??????????????? ??????? ??? ??????? ????????? ??? ???????? ?????????, ????? ?? ??????? ????????? ???????????? ????????????? ????? (???.5). ? ????? ????, ?????????, ??????? ??? ????????? ????????? ?? ???? ???????? ?????, ????? ???????? (?? ?????? ? ?????????, ?? ? ? ???????? ????????). ??????? ????????? ????????? - ?? ????????? (? ??????? ?? ????????? ????????? - ??????????) ??????????? ??? ?????????? ?????????. ????? ?? ????
состояний может быть отнесено к старости либо к не-старости.
|

|
В языке противоположным понятиям соответствуют антонимы - слова с противоположными значениями. Явление антонимии исключительно многообразно, оно далеко неоднозначно отражает виды логической противоположности. Например, на первый взгляд кажется, что только контрадикторность (но ни в коем случае не контрарность) связана в языке с применением отрицательной частицы «не» (рис.5). Но логическое и грамматическое отрицание - не одно и то же. При ближайшем рассмотрении обнаруживаются пары контрадикторных понятий, словесная форма которых не включает явного отрицания, скажем: «холостой - женатый». В то же время так называемое лексикализованное (слитое со словом) отрицание чаще всего выражает не контрадикторность, а контрарность, как это имеет место, например, в оппозиции «красивый - некрасивый».
Сложность логических и языковых механизмов, регулирующих отношения антонимии, с одной стороны, затрудняет контроль над смысловыми свойствами текста. С другой стороны, эта сложность - показатель богатства языка, источник совершенствования речи в плане
выразительности. Из литературных (стилистических в широком смысле слова) приемов, использующих антонимию, назовем антитезу, основанную на художественном «столкновении» противоположных (чаще всего контрарных) понятий, Эффект антитезы хорошо иллюстрируется следующими стихами М. И. Цветаевой: «Не люби, богатый, - бедную,/Не люби, ученый, - глупую,/Не люби, румяный, - бледную, /Не люби, хороший, - вредную!».
Подчинение (подчинённость).
|

 ???? ????? ??????? Q ??????? ?????? ? ????? ??????? Р ? ?????????? ??? ?????, ?? Р ?????????? ????????, ???????????? Q ,?Q - ????????, ???????????? Р (???.6). ????????? ?????????? (?????????????) ????????? ?????, ????????, ???????: ????????????????? ? ???????????? ???????????????, ????????? ? ????????, ???????????????? ? ?????????????? ?. ?. ?????????? "????"?. ??????? ???????????? ????? ??????? ????????? ? ??????? ???????????? ???????.
???? ????? ??????? Q ??????? ?????? ? ????? ??????? Р ? ?????????? ??? ?????, ?? Р ?????????? ????????, ???????????? Q ,?Q - ????????, ???????????? Р (???.6). ????????? ?????????? (?????????????) ????????? ?????, ????????, ???????: ????????????????? ? ???????????? ???????????????, ????????? ? ????????, ???????????????? ? ?????????????? ?. ?. ?????????? "????"?. ??????? ???????????? ????? ??????? ????????? ? ??????? ???????????? ???????.
Если оба понятия общие, то подчиняющее называют родовым (или просто родом), а подчинённое -видовым (просто видом). Из приведённых в предыдущем абзаце примеров первые два иллюстрируют родовидовое отношение: техническое редактирование - вид редактирования, газета - вид издания. В третьем примере подчиненное понятие - единичное, поэтому родовидового отношения здесь нет.
Следует подчеркнуть, что логическая квалификация какого-либо понятия как подчиняющего или подчинённого (для общих понятий - родового или видового) не является жесткой и теряет свое значение за пределами определенной пары множеств. Это, видно хотя бы из следующего отношения: «издание» - «газета» - «спортивная газета». Понятие, занимающее в этой цепочке среднюю позицию, подчинено предыдущему (и является для него видовым), но подчиняет последующее (и значит, становится в данном звене родовым). Вообще, отношения подчинённости (подчинения) могут охватывать неопределённо большое число понятий, например: «Спаниель» - «охотничья собака» - «собака» - «животное» и т. д.
Отношения между неопределенно большим количеством понятий.




|
Нужно отметить, что с увеличением количества рассматриваемых понятий возрастают трудности в построении графических схем, выражающих отношения между ними. Это и понятно: увеличивается число возможных областей пересечения классов, а значит, и тех «ячеек», которые должны на схеме соответствовать разным подмножествам.
|


 ??? ??? ??????? ???????, ??????????? ? ?????????? ??????????????, ?????????? ????????? ? ????????, ??? ??? ?? ???????? ?????? ????????? ?? ???????? ??????????? ????????? ?? ???????. ????????, ????????? ??????? ??????????, ???????????, ????????????, ????????? ??????????? ?????? (???.8). ????? ????????? 16 ???????????, ???????????????? ????? ?????????: 1)????????-??????????, ????????????? ??????????, ? ??????? ? ??????; 2) ????????-??????????, ???????????? ??????????, ?? ?? ??????? ? ??????; 3) ????????-???????????, ??????? ? ??????, ?? ?? ???????????? ???????, ?, 16) ????, ?? ?????????? ?? ??????????, ?? ????????????, ?? ?????????????, ?? ???????????.
??? ??? ??????? ???????, ??????????? ? ?????????? ??????????????, ?????????? ????????? ? ????????, ??? ??? ?? ???????? ?????? ????????? ?? ???????? ??????????? ????????? ?? ???????. ????????, ????????? ??????? ??????????, ???????????, ????????????, ????????? ??????????? ?????? (???.8). ????? ????????? 16 ???????????, ???????????????? ????? ?????????: 1)????????-??????????, ????????????? ??????????, ? ??????? ? ??????; 2) ????????-??????????, ???????????? ??????????, ?? ?? ??????? ? ??????; 3) ????????-???????????, ??????? ? ??????, ?? ?? ???????????? ???????, ?, 16) ????, ?? ?????????? ?? ??????????, ?? ????????????, ?? ?????????????, ?? ???????????.
Общая характеристика операций с понятиями.
Логические операции с понятиями - это такие действия, посредством которых из одного, двух или большего числа понятий образуется новое понятие. Иными словами, это действия, позволяющие определённым образом преобразовывать некоторые заданные множества.
|
|