Реферат: Поняття та класифікація систем радіоавтоматики

4.2 Статичні і динамічні властивості елементів

Після подачі на вхід елемента деякого впливу на його виході виникає перехідний процес, по закінченні якого настає стаціонарний стан.

Статична характеристика - це залежність, що зв'язує між собою стаціонарні вхідну і вихідну величини.

Прикладом статичної характеристики може служити залежність між напругою на виході частотного дискримінатора і відхиленням частоти сигналу від його номінального значення (рис.3).

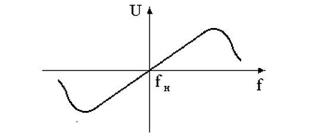
Рисунок 3 – Статична характеристика дискримінатора

Динамічна характеристика - це залежність, що зв'язує між собою зміни вхідної і вихідної величин у перехідному режимі.

4.3 Перетворення Лапласа

Перетворення Лапласа має дві взаємозалежні форми – пряму і зворотну.

Пряме перетворення описується так:

,

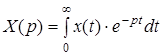де x(t) – оригінал функції, тобто функційна залежність у часовому вимірі;

x(p) –зображення функції x(t) за Лапласом, тобто у вимірі комплексної змінної

.

Зворотне перетворення вводиться у розгляд так:

,

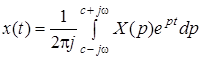що дозволяє відшукати оригінал функції x(t) по її зображенню X(p).

Існують такі методи відшукання оригіналу x(t): табличний та метод інтегрування у комплексній площині.

Глибинний сенс перетворення Лапласа полягає у тому, що за його допомогою стає можливим здійснити перехід від вихідних диференційних рівнянь, що описують систему РА у просторі комплексної змінної р .

На рис. 4 наведено загальну структурну схему ланки системи РА, яка описується коефіцієнтом передачі R(p). На цьому рисунку G(p) та x(p) – відповідно сигнали у операторній формі на вході і виході ланки.

Рисунок 4 – Загальна структурна схема ланки системи РА з коефіцієнтом передачі R(p) у операторній формі.

Наприклад, якщо ланка є диференціатором, то R(p)=p.

Тоді Якщо ланка є інтегратором, то

Тоді

4.4 Перетворення Фур'є

Якщо в перетворенні Лапласа замінити оператор р на змінну jw отримаємо перетворення Фур'є, яке також поділяється на пряме та зворотне.

Для прямого перетворення Фур'є маємо вираз

,