Реферат: Последовательности одиночных сигналов. Монохроматический и принятый сигнал
имеет единственную спектральную составляющую на частоте ω0 (рис. 8).
Функция неопределённости монохроматического сигнала имеет единственный лепесток, бесконечно узкий вдоль оси частот и бесконечно широкий вдоль оси времени (рис. 9).

Рис. 6. Монохроматический сигнал.
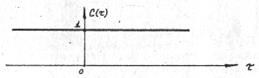
Рис. 7. Корреляционная функция закона модуляции монохроматического сигнала.

Рис. 8. Энергетический спектр монохроматического сигнала.
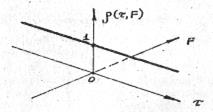
Рис. 9. Функция неопределённости монохроматического сигнала.
Принятый сигнал
Принятый сигнал
![]()
имеет не только первичную регулярную модуляцию ![]() , но и приобретенную в результате отражения, рассеяния, распространения радиоволн вторичную случайную модуляцию
, но и приобретенную в результате отражения, рассеяния, распространения радиоволн вторичную случайную модуляцию ![]()
Корреляционная функция принятого сигнала представляется как результат двухэтапного усреднения - статистического усреднения случайной временной структуры (обозначается чертой сверху) и усреднения регулярной временной структуры: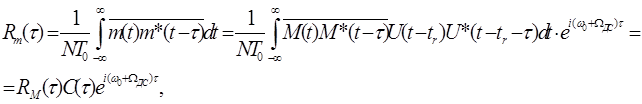
где ![]()
есть корреляционная функция комплексной огибающей принятого сигнала. Статистическое усреднение комплексной огибавшей M(t) , являющейся согласно физическим представлениям эргодическим случайным процессом (для которого усреднение по времени и по ансамблю реализаций эквивалентны), предполагает усреднение по множеству реализаций, продолжительность которых ограничена временем наблюдения объекта наблюдения (сигнала) в пределах одного элемента разрешения. Иными словами, статистическое усреднение предполагает усреднение по множеству реализаций. Корреляционная функция комплексной огибающей М(t) является характеристикой как амплитудных, так и фазовых его флуктуации. Она определяется экспериментально. Результаты многочисленных экспериментальных исследований свидетельствуют о возможноcти её аппроксимации удобной в практических приложениях экспоненциальной кривой (рис. 10): ![]() где
где 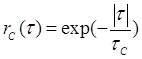 - нормированная корреляционная функция флуктуации принятого сигнала.
- нормированная корреляционная функция флуктуации принятого сигнала.
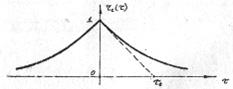
Рис. 10. Нормированная корреляционная функция флуктуаций принятого сигнала.
Время корреляции флуктуации принятого сигнала τ0 зависит от многих факторов (диапазона частот, размеров объекта наблюдения, динамики его движения, условий распространения радиоволн и др.) и может изменяться в широком диапазоне от единиц миллисекунд до единиц секунд.
Таким образом, корреляционная функция принятого сигнала окончательно может быть представлена следующим выражением:
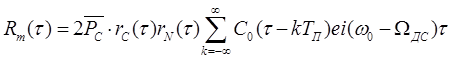
Она отличается от корреляционной функции излучаемой нефлуктуирующей ограниченной последовательности одиночных сигналов наличием дополнительного сомножителя r0 (τ) . Произведение rN (τ) * rc (τ) характеризует нормированную корреляционную функцию огибающей ограниченной по времени и флуктуирующей по амплитуде и фазе последовательности одиночных сигналов:
![]() .
.
Энергетический спектр принятого сигнала представляется произведением энергетического спектра одиночного сигнала и междупериодного энергетического спектра флуктуирующей ограниченной последовательности
![]()
причем гребенчатый междупериодный энергетический спектр есть размноженный по частоте с интервалом, равным частоте повторения, энергетический спектр огибающей последовательности с учетом ограниченного времени наблюдения и флуктуации:

Ширина зубцов энергетического спектра принятого сигнала, т.е. ширина энергетического спектра огибающей последовательности, определяется, во-первых, величиной, обратной времени наблюдения (продолжительности последовательности) и, во-вторых, спектра флуктуации принятого сигнала:

Вероятностные свойства принятого сигнала определяются вероятностными характеристиками его комплексной огибающей. Наиболее полной характеристикой комплексной огибающей принятого сигнала, которая вместе с тем является необходимой при решении целого ряда задач синтеза и анализа РТС, является многомерная плотность вероятности значений этого процесса, взятых в дискретные моменты времени.

Рис. 11. Совместное распределение квадратурных составляющих комплексной огибающей принятого сигнала.
Поэтому совместное распределение вероятности квадратурных составляющих комплексной огибающей принятого сигнала определяется выражением

и изображается колоколообразной поверхностью (рис. 11).
Совместная плотность вероятности квадратурных составляющих представляется произведением одномерных нормальных (гауссовых) распределений вероятности каждой квадратурной составляющей
