Реферат: Постановка задачі оптимального керування

2. Якщо задані початкові і кінцеві умови , то задача оптимального керування називається двоточковою задачею або задачею з фіксованими кінцями. При цьому інтервал часу керування може бути заданий або підлягає визначенню. Для даної задачі множина мети керування складається з єдиної точки .

3. Якщо значення координат (всіх або частини) вектора стану задані для декількох фіксованих моментів часу , , …, , то задача оптимального керування називається багатоточковою задачею керування.

4. У задачах з рухомими кінцями необхідно визначити керування, що переводить об'єкт із деякого заздалегідь невідомого стану в деякий стан , де множини , відомі. Якщо і вироджуються в точки, то задача оптимального керування стає задачею із фіксованими кінцями.

Якщо час і початкових і кінцевих крайових умов і відомий, то задача оптимального керування називається задачею з фіксованим часом. Якщо ж невідомо, то задача називається задачею з вільним часом.

3. Критерії якості

Найчастіше задача керування має безліч розв’язків, тобто існує безліч керувань, які дозволяють досягти бажаної мети. У такому випадку виникає задача, як серед всіх припустимих керувань вибрати таке, для якого керований процес буде, в певному розумінні, найкращим. Інакше кажучи, якщо якість процесу можна оцінити деякою числовою характеристикою – критерієм якості, то задача полягає у виборі такого керування, що забезпечить його оптимальне значення. Далі вважатимемо, що оптимальним є мінімальне значення критерію . Отже, задача оптимального керування полягає в тому, щоб визначити таке керування

, що реалізує ціль, і для якого функціонал набуває найменшого можливого значення:

.(4)

Процес з (4) називається оптимальним процесом, а відповідні йому керування і фазова траєкторія – оптимальним керуванням і оптимальною траєкторією.

Припустимий процес називається локально оптимальним у задачі з фіксованим часом , якщо для певного і для будь-якого припустимого процесу , що задовольняє умові

, ,

має місце нерівність .

Якщо відрізок не фіксований, то локально оптимальним процесом називається припустимий процес на інтервалі часу , для якого існує таке , що для будь-якого процесу , заданого на інтервалі часу , такого що

, , , ,

має місце умова .

Існують такі типи критеріїв якості.

Для керування процесами (3) найчастіше використовуються інтегральні критерії:

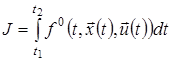.(5)

Інтегральні критерії розділяються на:

а) інтегральний критерій оптимальної швидкодії:

з підінтегральною функцією ;

б) інтегральний квадратичний критерій з підінтегральною функцією

,

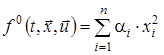де ;

, – коефіцієнти, серед яких є хоча б один ненульовий.

Вивчення системи може проводитися як на скінченному, так і на нескінченному інтервалі часу, тому в інтегралі (5) ;

в) енергетичні критерії якості з підінтегральними функціями

або ,

де ;