Реферат: Построение интерполяционного многочлена и вычисление по нему значения функции для заданного аргумента

Глава 1

Основные направления исследования: разрешимость задачи интерполирования, простейших интерполяционных формул, применение интерполяции для построения приближенных интерполяционных формул, применение интерполяции для построения приближенных и численных методов решения различных задач математики и ее приложений.

Приближенное представление функций. Интерпояционные функции на отрезке по значениям ее в узлах сетка - означает постоение другой функции такой, что В более общей постановке задача интерполирования функции состоит в постоении не только из условий совпадения значений функций и на стеке , но и совпадения в отдельных узлах производных до какого-то порядка или некоторых других соотношений, связанных и .

Обычно стоится в виде

,

где - некоторая заранее выбранная система линейно независимых функций. Такое интерполирование называется л и н е й н ы м относительно системы , а интерполяционным многочленом по системе .

Выбор системы определяется свойством класса функций, для приближения которого предназначаются интерполяционные формулы. Например, для приближения - периодической функции на за естественно взять тригонометрическую систему функций, для приближения на полу оси ограниченных или возрастающих функции- систему рациональных или показательных функций, учитывающих поведение приближаемых функций на бесконечности и т.д.

Чаще всего используя а л г е б р а и ч е с к о е интерполирование: . Существует ряд явных представлений алгебраических интерполяционных многочленов. Например интерполяционный многочлен Лагранжа имеет вид:

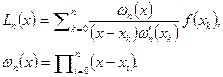
В задаче приближения функции и на всём отрезке алгебраическое интерполирование высокого порядка выполняется сравнительно редко. Алгебраический интерполяционный процесс не является сходящимся в классе непрерывных на функций. Обычно ограничиваются линейным интерполированием по узлам и на каждом отрезке или квадратичным по трем узлам ,, на отрезке .

Эффективным аппаратом приближения функции являются интерполяционные сплайны, но их построение в ряде частных случаях требует значительных вычислительных затрат.

На практике чаще всего используются параболические или кубические полиноминальные сплайны. Интерполяция кубическим сплайном дефекта 1 для функции относительно сетки называет функцию , являющуюся многочленом 3-й степени на каждом из отрезков , принадлежащую классу дважды непрерывно дифференцируемых функции и удовлетворяющую условиям

.

При таком определении кубического сплайна, он имеет еще свободных параметра, для нахождения которых на сплайн налагаются дополнительные краевые условия. Например или и , или некоторые другие.

Полиномиальный интерполяционный сплайн произвольной степени m дефекта r определяется как функция , удовлетворяющая, кроме условий и , еще дополнительно условиям совпадения в узлах сетки значений функции и интерполированной функции и их производных до некоторого порядка.

Часто при обработке эмпирических данных коэффициенты в определяют исходя из требования минимизации суммы

- заданные числа, .

Такое построение функции называют интерполированием по методу наименьших квадратов.

Интерполирование функций многих переменных имеет ряд принципиальных и алгебраических трудностей. Например в случае алгебраической интерполяции интерполяционный многочлен Лагранжа фиксированной степени, вообще говоря, не существует для произвольной схемы различных узлов интерполяции. В частности для функций двух переменных такой многочлен суммарной степени не выше n может быть построен по узлам лишь при условии, что эти узлы не лежат на алгебраической кривой порядка n .

Другой поход к интерполированию функции многих переменных стоит в том, что сначала интерполируется функция по переменной при фиксированных потом по следующей переменной при фиксированных и т.д. интерполяционные сплайны для функций многих переменных определяются по многомерной сетке при соответствующих изменениях по аналогии с одномерным случаем.

Интерполирование функций и численные методы. Интерполирование функции используется:

1. для замены сложно вычисляемой функции другой, вычисляемой проще

2. для приближенного восстановления функции на всей области задания по значениям её в отдельных точках или по другим известным величинам

3. для получения сглаживающих функций

4. для приближенного нахождения предельных значений функции

5. в задачах ускорения сходимости последовательностей и рядов и в других вопросах.

Общие идеи построения интерполяционных методов решения уравнения =0 и систем уравнения , одни и те же. Трудности задачи интерполирования функций многих преременных особенно сказывается при исследовании и практическом использовании такого рода методов для большого числа уравнений. В основу получении интерполяционных методов решения уравнения =0 положена замена функции ее интерполяционным многочленом и последующим решением уравнения =0 берутся за приближенные решении уравнения =0 интерполяционный многочлен используется так же при построении итерационных методов решения уравнения =0 .

Например взяв за корень линейного интерполяционного алгебраического многочлена, построенного по значениям и в узле или по значениям и в узлах и , приходят соответственно к методу Ньютона и метода секущих