Реферат: Поверхности спроса
В подавляющем большинстве случаев на практике приходится иметь дело с классической формой кривой спроса вот по каким причинам. Реальная цена за единицу товара, которую предлагает его производитель, не может быть ниже ее себестоимости Р0. Значит, из изображенной на рисунке 5 кривой будет "работать" не вся кривая спроса, а только та ее часть, которая лежит правее точки Р0. Но, как следует из графика рисунка 5, участок кривой спроса при ценах выше себестоимости ведет себя классическим образом. Именно поэтому на практике поведение потребителя, подобно первому участку кривой спроса рисунка 5, лежащего в области цен от нуля до Р0, встречается очень редко.
Есть еще одно интересное замечание. Если увеличивать доход и получать соответствующие ему кривые спроса, то можно получить при большом доходе очень интересную кривую спроса, которая на значительном участке непрерывно и почти линейно возрастает, а классический участок (убывания объема при увеличении цены) уходит в бесконечность (рисунок 6).

Рисунок 6. Начальный участок кривой спроса при доходе, значительно превышающем Сtr
В этом случае повышение цен на товар всегда будет приводить к росту объемов его приобретения. Причем резкие колебания цен не будут приводить к значительному изменению поведения потребителя. И лишь в том случае, когда цена на товар будет очень велика, поведение спроса будет соответствовать его известному характеру. Такие случаи следует признать очень редкими и, забегая вперед, характерными для некоторых товаров в высокоразвитых странах.
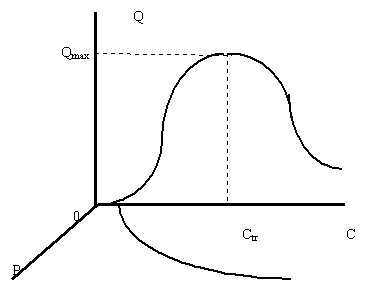
Рисунок 7. Предварительный вид поверхности спроса в пространстве объем-цена-доход для товара, не являющегося предметом повседневного спроса
Рассмотрю теперь поверхность спроса для другого случая, когда товар не является предметом повседневного спроса. В этом случае для построения поверхности спроса необходимо воспользоваться рисунком 1.2.5 и 1.3.2.
Их синтез, полученный аналогично тому, как был получен график рисунка 1, дает первое представление о характере поверхности (рисунок 7). Как легко убедиться из графика рисунка 7, поверхность спроса в данном случае имеет очень сложную форму. В зависимости от того, насколько эта поверхность полога, можно предположить существование двух типов поверхностей.
Первая поверхность получается, если поверхность спроса имеет резкий уклон к плоскости цена-доход. В данном случае ее сечения плоскостями, параллельными плоскости цена-объем, может привести к результатам, изображенным на рисунке 8, при пересечении плоскостей и поверхности спроса получаются классические кривые спроса, их максимум в рассматриваемом пространстве находится на плоскости объем-доход, то есть в точках с нулевой ценой. На рисунке 8 показан пример такого сечения плоскостью, обозначенной цифрами 1-1.
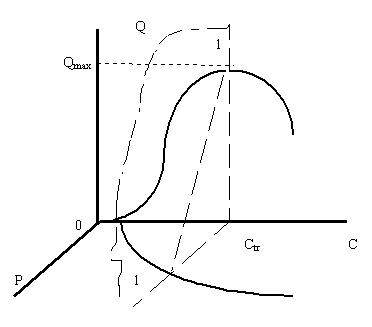
Рисунок 8. Сечение плоскостью постоянных доходов поверхности спроса для товара, не являющегося предметом повседневного спроса
Для удобства анализа на плоскости проведен отрезок прямой, который выходит из точки, лежащей на плоскости объем-доход и заканчивающийся на плоскости цена-доход (показана линией крупным пунктиром). Все точки кривой спроса на этой плоскости лежат ниже этого отрезка.
С увеличением дохода кривые спроса будут как бы "придавливаться" к плоскости цена-доход и при достижении определенной величины дохода совпадут с плоскостью цена-доход - товар для покупателя с такими доходами становится не интересен.
Товарами, которые имеют такой характер поверхности спроса, могут быть предметы, не носящие престижный характер, обладание которыми удовлетворяет какую-либо потребность, но объемы их не свидетельствуют о социальном статусе его обладателя и вполне могут быть заменены некоторым альтернативным товаром. Именно поэтому увеличение цены на этот товар приводит к уменьшению объемов его потребления для покупателей с любыми доходами - кривая спроса ведет себя "классическим" способом. По-видимому, к такому товару следует отнести предметы роскоши, которые многообразны и альтернативны.
Следующим вариантом поверхности спроса для товара, не являющегося предметом повседневного спроса, может быть случай, когда уклон поверхности спроса имеет не пологий характер, а изменяется так, как это изображено на рисунке 1.2.5, причем уменьшение величины объемов с увеличением цены и дохода очень значительно.
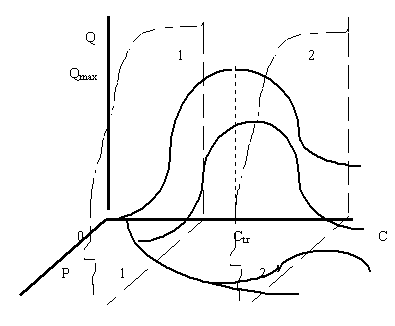
Рисунок 9. Второй вариант сечения плоскостью постоянных доходов поверхности спроса для товара, не являющегося предметом повседневного спроса
В этом случае поверхность спроса будет иметь более сложный нелинейный характер, чем тот, который был только что изучен (рисунок 9). Сечение этой поверхности плоскостями постоянного дохода приведет к получению кривых спроса нескольких видов.
Рассмотрим для определенности два возможных случая, принципиально отличных друг от друга. На рисунке 9. эти два случая определяются пересечением поверхности спроса двумя различными плоскостями постоянного дохода, обозначенных на рисунке соответственно цифрами 1-1 и 2-2.
Если доход не превышает величины Сtr, то сечение поверхности спроса плоскостями постоянного дохода будет давать классические кривые спроса.
Если же доход превышает величину Сtr, то кривые спроса будут иметь в результате сечения поверхности спроса плоскостями постоянного дохода форму наподобие формы рисунка 5. С дальнейшим увеличением дохода эти кривые совпадают с плоскостью доход-цена. Таким образом, в отличие от случая рисунка 8, где получались в результате сечения только классические кривые спроса, в последнем случае встречаются кривые более сложного характера.