Реферат: Поверхностное натяжение и адсорбция на границе вода-воздух
Видно, что наиболее сильно поверхностное натяжение снижается при низких концентрациях для полимера с наибольшей молекулярной массой, причем ход зависимости аналогичен кривым изменения поверхностного натяжения растворов поверхностно-активных веществ
Равновесное поверхностное натяжение
К простым способам измерения поверхностного натяжения относится метод кольца дю Нуи. Платиновое кольцо притапливают в жидкости, и измеряется сила, необходимая для вытягивания кольца через поверхность. Вместо кольца можно использовать платиновую пластинку. Измеряют силу втягивания пластинки в жидкость, эта сила зависит от краевого угла смачивания пластины жидкостью. Очень простым методом измерения поверхностного натяжения является измерение подъема смачивающих жидкостей в капиллярах. Высота подъема hпрямо пропорциональна поверхностному натяжению согласно уравнению г = rhpg/2, где г—радиус капилляра, с — плотность жидкости, g— ускорение свободного падения. Это уравнение справедливо только для жидкостей, идеально смачивающих стенки капилляра, т. е. когда краевой угол смачивания равен нулю.
В некоторых системах равновесное состояние устанавливается очень долго, и измерения поверхностного натяжения в этих случаях занимают длительное время. К таким системам относятся растворы высокомолекулярных ПАВ. Для подобных систем приемлемым методом измерения является метод висящей капли. Мерой поверхностного натяжения в этом случае служит форма капли; капли, близкие к сферическим, образуются из жидкостей с большим поверхностным натяжением, удлиненные капли образуются из жидкостей с низким поверхностным натяжением. Этот метод пригоден также для измерения межфазного натяжения между двумя взаимно нерастворимыми жидкостями.
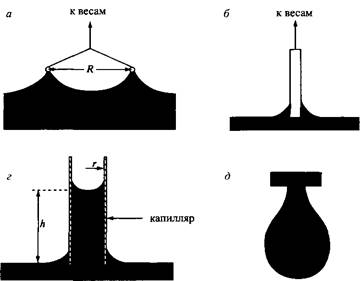
Рис. 11. Поверхностное натяжение можно измерить: методом дю Нуи, методом пластинки Вильгельми, методом подъема жидкости в капилляре, методом висящей капли
Динамическое поверхностное натяжение
Динамическое поверхностное натяжение можно измерять различными способами, например методом наибольшего давления в пузырьке. Воздух непрерывно пропускается через два капилляра различных диаметров, погруженных в раствор. Давление, которое требуется для образования пузырька, обратно пропорционально диаметру капилляра и прямо пропорционально поверхностному натяжению жидкости. Использование двух капилляров позволяет не измерять глубину погружения капилляра в жидкость. Данным методом измеряют динамическое поверхностное натяжение в интервалах времени 1-10 мс. При необходимости измерять динамическое поверхностное натяжение в еще более коротких интервалах используют метод осцилляции струи. Жидкая струя испускается из отверстия эллиптической формы.
Из-за некругового поперечного сечения струя механически неустойчива, жидкость в струе стремится принять круговое поперечное сечение, что приводит к осцилляции сечения между предельными значениями. Частота таких осцилляции связана с динамическим поверхностным натяжением.
Поверхностное и межфазное натяжения как результат межмолекулярных взаимодействий
Обсудим зависимость поверхностного и межфазного натяжения от особенностей взаимодействия между молекулами. Для простоты изложения энтропийные вклады в поверхностное натяжение можно не учитывать. Запишем энергию, приходящуюся на молекулу в объеме жидкости А, как
![]()
где Waa— отрицательная величина, характеризующая энергию притяжения между молекулами. Обозначим долю ближайших соседей в плоскости, параллельной поверхности, как /, а долю ближайших соседей в плоскости, расположенной над ней или под ней — как т. Тогда можно записать
![]()
Энергия на одну молекулу на поверхности вода-воздух описывается соотношением
![]()
так как в плоскости над поверхностью вода-воздух у молекулы нет соседей. Энергия, необходимая для переноса одной молекулы из объема на поверхность, выражаться тогда как
![]()
Поскольку энергия Waa— отрицательная величина, очевидно, что для переноса молекулы из объема на поверхность требуются источники положительной энергии. По этой причине капля жидкости принимает сферическую форму, достигая таким образом минимальной площади поверхности и, следовательно, минимальной полной энергии системы.
Величина AEв уравнении, будучи нормированной на площадь поперечного сечения молекулы яa9 равна поверхностной энергии. Поскольку в данном обсуждении мы пренебрегли энтропийными вкладами, эта величина равна свободной поверхностной энергии или поверхностному натяжению:
![]()
Уравнение еще раз показывает, что поверхностное натяжение жидкости является следствием энергии когезии жидкости.
Межфазное натяжение характеризует не только энергию когезии двух жидкостей, находящихся в контакте друг с другом, но также и взаимодействие между этими жидкостями или, точнее, взаимодействие между разными молекулами. Как и ранее, запишем энергию, приходящуюся на молекулу в обеих жидких фазах, как
![]()
![]()
Энергия, приходящаяся на молекулу типа А или В на межфазной границе AB, выражается соотношениями
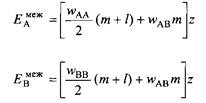
Энергия, необходимая для создания поверхности, выраженная на единицу площади поверхности, равна межфазному натяжению:
Из уравнения следует, что межфазное натяжение пропорционально параметрам wили ч, т. е. определяется различием свойств этих жидкостей. Так, если данная пара жидкостей сильно различается по свойствам, их межфазное натяжение будет большим как, например, в системе вода-алифатический углеводород. Если же жидкости более совместимы, межфазное натяжение будет уменьшаться и в пределе может стать равным нулю. Приведенный анализ является некоторым приближением, поскольку в нем не учитывалась взаимная растворимость жидкостей и игнорировались энтропийные вклады. Работа адгезии Wqмежду двумя материалами определяется вкладами межфазной и поверхностной энергии:
![]()
С учетом уравнений и, работу адгезии можно записать в следующем виде: