Реферат: Преобразования фигур

AB² =(x₂ -x₁ )² +(y₂ -y₁ )²

A'B'² =(-x₂ + x₁ ) ² +(y₂ -y₁ )²

Отсюда видно, что AB=A'B'. А значит, что преобразование симметрии относительно прямой есть движение. Теорема доказана.

Симметрия относительно плоскости

Пусть a - произвольная фиксированная плоскость. Из точки X фигуры опускаем перпендикуляр XA на плоскость a и на его продолжении за точку Aоткладываем отрезок AX', равный XA. Точка X' называется симметричной точке X относительно плоскости a, а преобразование, которое переводит X в симметричную ей точку X', называется преобразованием симметрии относительно плоскости a.

Если точка X лежит в плоскости a, то считается, что точка X переходит в себя. Если преобразование симметрии относительно плоскости a переводит фигуру в себя, то фигура называется симметричной относительно плоскости a, а плоскость a называется плоскостью симметрии этой фигуры.

Поворот

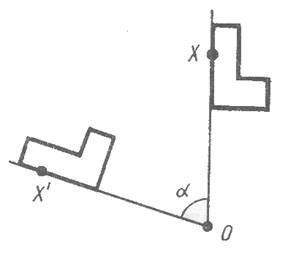Поворот плоскости около данной точки называется такое движение, при котором каждый луч, исходящий из точки, поворачивается на один и тот же угол в одном и том же направлении.
Это значит, что если при поворот около точки O точка переходит в точку X', то лучи OX и OX' образуют один и тот же угол, какова бы ни была точка X. Этот угол называется углом поворота . Преобразование фигур при повороте плоскости также называется поворотом .

Параллельный перенос в пространстве

Параллельным переносом в пространстве называется такое преобразование, при котором произвольная точка (x; y; z) фигуры переходит в точку (x+a; y+b; z+c), где числа a,b,c одни и те же для всех точек (x; y; z). Параллельный переносов пространстве задается формулами

x'=x+a, y'=y+b, z'=z+c,

выражающими координаты x', y', z' точки, в которую переходит точка (x; y; z) при параллельном переносе. Так же, как и на плоскости, доказываются следующие свойства параллельного переноса:

1. Параллельные перенос есть движение.

2. При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.

3. При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя).

4. Каковы бы ни были точки A и A', существует единственный параллельный перенос, при котором точка A переходит в точку A'.

Новым для параллельного переноса в пространстве является следующее свойство:

5. При параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в параллельную её плоскость.

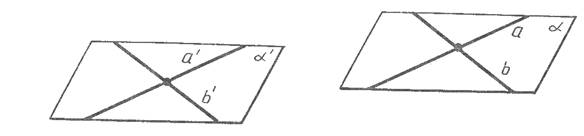
Действительно, пусть a - произвольная плоскость, проведем в этой плоскости две пересекающиеся прямые a и b. При параллельном переносе прямые a и b переходят либо в себя, либо в параллельные прямые a' и b'. Плоскость a переходит в некоторую плоскость a', проходящую через прямые a' и b'. Если плоскость a' не совпадает с a, то по теореме о двух пересекающихся прямых одной плоскости соответственно параллельными с пересекающимися прямыми другой плоскости, она параллельна a, что и требовалось доказать.

Список использованной литературы:

1. Учебник Геометрии 7-11 классы. А.В. Погорелов

2. Учебник Геометрии 10-11 классы. А.Д. Александров.