Реферат: Прямая Эйлера
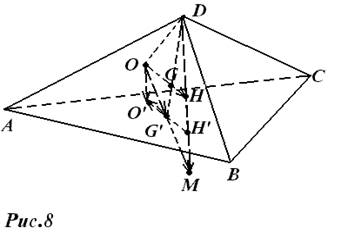
Доказательство. Пусть ABCD – ортоцентрический тетраэдр, DG’ – его медиана, DH’ – его высота (рис.8). Тогда G’ центроид, а H’- ортоцентр треугольника ABC, причем точки O’ ( центр окружности, описанной около треугольника ABC ), G’ и H’ лежат на одной прямой. Заметим, что центр O сферы, описанной около тетраэдра ABCD, лежит на перпендикуляре к плоскости треугольника ABC, восстановленном в точке O’.
Будем доказывать теорему тем же способом, что и теорему 2 для треугольника: строить разными способами точку H, удовлетворяющую соотношению (5).
Вначале сложим векторы OA, OB и OC:
OM = OA + OB + OC.
По теореме 1
OG’ = -- (OA + OB + OC),
поэтому
OM = 3OG’
-7-
или G’M = 2OG’ . Точки O’,G’,H’, лежат на прямой Эйлера треугольника ABC, причем H’G’ = 2G’O’. Следовательно,
H’M=H’G’+G’M’=2(G’O’+OG’)=2(OG’+G’O’)=2OO’.
Отсюда вытекает, что прямые H’M и OO’ параллельны, а так как прямая OO’ перпендикулярна к плоскости ABC, то и прямая H’M перпендикулярна к этой плоскости. Следовательно, точка M’ лежит на прямой DH’ ( если точки O и O’ совпадают, то точки M и H’ тоже совпадают).
Пусть теперь
OH= --- (OM+OD)= ---(OA+OB+OC+OD).
Из левого равенства следует, что точка H является серединой отрезка DM, т.е. точка H лежит на DH’ тетраэдра.
Аналогично строится точка N: ON=OA+OB+OD и та же точка H: OH= --(ON+OC) и доказывается, что точка H лежит на высоте тетраэдра, проведенной из вершины C, и т.д.
Следовательно, высоты ортоцентрического тетраэдра пересекаются в одной точке H, определяемой соотношением (5).
Прямая Эйлера тетраэдра.
Теорема 6. Центр О описанной сферы, центроид G и ортоцентр Н ортоцентрического тетраэдра ABCD лежат на одной прямой, причем точки О и Н симметричны относительно точки G.
Доказательство. По формулам (4) и (5)
OH= -- (OA + OB + OC +OD),
OG= -- (OA + OB + OC + OD),
откуда OH=2OG. Полученное равенство означает, что точки O, G, H лежат на одной прямой, причем точки О и Н симметричны относительно точки G.
Прямую, на которой лежат точки O, G, H, можно назвать прямой Эйлера ортоцентрического тетраэдра.
В данном реферате собран материал необходимый для выявления прямой Эйлера и прямой Эйлера тетраэдра .
Использованные источники информации:
1. “Прямая Эйлера” (Э. Готман).
2. Международная информационная сеть Internet (URL: http://www.referat.ru; http://dlc.miem.edu.ru/referat ).
-9-