Реферат: Применение фильтра Калмана в задаче идентификации отказов двигателей стабилизации космического аппарата
У статті запропонований алгоритм контролю функціонування системи управління космічного апарата, який побудовано на основі субоптимального фільтра Калмана. Алгоритм дозволяє за інформацією безплатформеної інерційної навігаційної системи ідентифікувати відмови двигунів стабілізації, у тому числі, відмови з неповною потугою при наявності шумів вимірювання та дії зовнішніх обурюючих впливів.
The monitoring algorithm of functioning of a spacecraft control system, constructed on the basis the suboptimum Kalman filter, is offered. The algorithm allows under the information of the platformless inertial navigation system to identify the stabilization engines' failures, including failures with incomplete draft at presence of measurements noise and action of external perturbation influences.
Отказ реактивных двигателей стабилизации (ДС) системы управления космического аппарата (КА), может приводить к не выполнению целевой задачи, а отказ типа «неотключение» двигателя, может приводить к большим потерям рабочего тела и раскрутке КА до недопустимых угловых скоростей.
Существующие методы контроля работоспособности ДС [1, 2, 4] являются достаточно грубыми, чтобы выявлять отказ типа "неотключение" при наличии остаточной неполной тяги двигателя на фоне действия внешних возмущающих моментов (гравитационных, аэродинамических и др.). Поэтому разработка алгоритмов идентификации отказов двигателей стабилизации, особенно отказов с неполной тягой при наличии шумов измерений и действии внешних возмущающих воздействий, является актуальной задачей.
В настоящей статье для построения алгоритма идентификации отказов ДС предлагается использовать фильтр Калмана.
В процессе исследований космический аппарат рассматривается, как абсолютно твердое тело, не содержащее каких-либо движущихся масс [1]. Если триэдр жестко связанных с телом осей Oxyz (связанная система координат - ССК) направить так, чтобы они совпали с главными центральными осями инерции, то центробежные моменты инерции обратятся в нуль и система уравнений Эйлера, описывающая динамику вращения КА вокруг центра масс, примет вид:
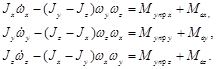 (1)
(1)
Здесь w j – проекции вектора абсолютной угловой скорости тела на оси ССК; Мупрj , Мвj - управляющий и возмущающий моменты соответственно; Jj - главные центральные моменты инерции тела относительно связанных осей; j=x, y, z .
Наряду с динамическими уравнениями рассматриваются кинематические уравнения, связывающие угловые скорости w j с углами поворота триэдра осей Oxyz относительно триэдра осей некоторой базовой системы координат (БСК), начало которой совпадает с началом координат ССК, а оси определенным образом ориентированы в инерциальном пространстве и движутся поступательно. Пусть углы ориентации (углы Эйлера-Крылова) ![]() – полностью определяют угловое положение ССК относительно БСК. Понятие углов ориентации становится однозначным лишь после того, как введена последовательность поворотов твердого тела вокруг осей Ox, Oy, Oz. Для последовательности поворотов:
– полностью определяют угловое положение ССК относительно БСК. Понятие углов ориентации становится однозначным лишь после того, как введена последовательность поворотов твердого тела вокруг осей Ox, Oy, Oz. Для последовательности поворотов: ![]() система кинематических уравнений имеет вид:
система кинематических уравнений имеет вид:
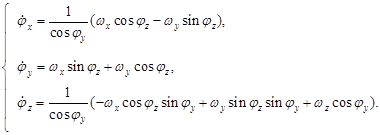 (2)
(2)
Системы (1) и (2) описывают угловое движение твердого тела относительно БСК. Будем предполагать, что углы Эйлера-Крылова j j малы. Текущие значения w j оцениваются в системе по информации измерителя угловой скорости, измеряющего интегралы от проекций вектора абсолютной угловой скорости КА на оси чувствительности прибора.
Интегрируя кинематические уравнения (2) в бортовой цифровой вычислительной машине (БЦВМ) при начальных значениях углов![]() , и интегрируя уравнения движения центра масс КА при соответствующих начальных условиях, реализуют бесплатформенную инерциальную навигационную систему (БИНС). Таким образом, считаем, что текущие величины углов j j непрерывно вычисляются в БИНС.
, и интегрируя уравнения движения центра масс КА при соответствующих начальных условиях, реализуют бесплатформенную инерциальную навигационную систему (БИНС). Таким образом, считаем, что текущие величины углов j j непрерывно вычисляются в БИНС.
Момент Мупрj формируется в соответствии с логикой закона управления и обеспечивает заданное угловое положение КА. Источником внешнего возмущающего момента Мвj , является взаимодействие КА с внешней средой, приводящее к появлению действующих на корпус внешних сил – гравитационного, аэродинамического, светового, магнитного [4].
Закон управления формируется путем сложения позиционного сигнала j j и скоростного сигнала w j , умноженного на коэффициент усиления k j (j = x , y , z ):
![]() . (3)
. (3)
Считаем, что двигатели стабилизации установлены попарно в каждом канале управления и на участке поддержания ориентации работают в импульсном режиме [1]. Включение двигателей происходит при выполнении условия ![]() , где
, где ![]() - зона нечувствительности.
- зона нечувствительности.
Алгоритм обработки данных в бесплатформенной инерциальной навигационной системе строится с использованием субоптимального дискретного фильтра Калмана [3].
Для малых угловых отклонений осей ССК от БСК и при условии Ix » Iy » Iz уравнения (1) и (2) запишем в виде:
![]()
Тогда для построения системы оценки вектора состояния (j j , w j , m в j ) примем следующую модель объекта наблюдения:
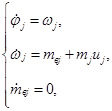 (4)
(4)
где mj =МДС j / Jj - эффективность управляющего момента;
МДС j - управляющий момент ДС;
m в j =Мв j / Jj - эффективность возмущающего момента;
uj - сигнал управления ДС;
j=x , y , z.
Запишем систему уравнений (4) в стандартной векторно-матричной форме, дополнив ее уравнением измерений:
![]()
где xj = (x 1 j , x 2 j , x 3 j )T =(j j , w j , m в j )T - вектор состояния;
zj - вектор измерений;
x j - шум измерений;
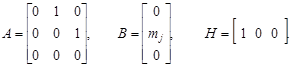 ,
,
j =x , y , z .
Используя критерий Калмана, несложно показать, что такая система является полностью наблюдаема:
rank[HT AT HT (AT )2 HT ]=n=3, где n - порядок системы.
Реализация в бортовом вычислителе дискретного фильтра Калмана сводится к оценке вектора состояния по следующим соотношениям:
![]()
--> ЧИТАТЬ ПОЛНОСТЬЮ <--