Реферат: Применение резистивных электрических цепей в радиотехнических устройствах
Поскольку ток ![]() известен и
известен и ![]() , то окончательно получим:
, то окончательно получим:
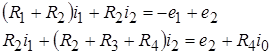 .
.
Метод контурных токов целесообразно применять тогда, когда число контурных уравнений оказывается меньшим числа узловых уравнений.
Решение системы контурных уравнений.
Теорема взаимности
В общей форме система уравнений контурных токов, или система контурных уравнений, может быть записана в следующем виде:
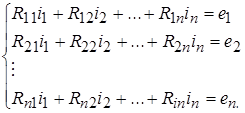
![]()
Если число уравнений получилось достаточно большим, то для решения системы уравнений применяются известные из математики методы, например, метод Крамера. Все n уравнений являются линейно-независимыми и поэтому система разрешима относительно n искомых токов. В этом случае контурный ток k–го контура определяется следующим образом:
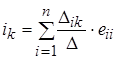 ,
,
где ![]() – определитель системы контурных уравнений;
– определитель системы контурных уравнений; ![]() – алгебраическое дополнение элемента
– алгебраическое дополнение элемента ![]() определителя.
определителя.
Общее решение для k-го контурного тока имеет вид:
![]() .
.
Отсюда следует, что контурный ток можно найти как алгебраическую сумму частных токов, создаваемой каждой ЭДС ![]() , в отдельности. Данное соотношение есть математическая запись принципа наложения, справедливого для линейных цепей.
, в отдельности. Данное соотношение есть математическая запись принципа наложения, справедливого для линейных цепей.
На основании общего решения системы контурных уравнений можно доказать следующую теорему: если источник напряжения, включенный в первый контур пассивной цепи, вызывает во втором контуре ток ![]() , то тот же источник, будучи включенным во второй контур, вызовет в первом контуре такой же ток i .
, то тот же источник, будучи включенным во второй контур, вызовет в первом контуре такой же ток i .
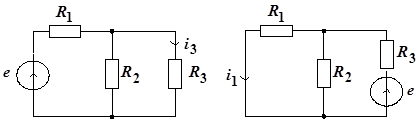 |
Рис. 1.3.
Дуальная формулировка этой теоремы такова: если источник тока, включенный к первой паре узлов пассивной цепи, вызывает между второй парой узлов этой цепи некоторое напряжение и, тот же источник, будучи включенным, к этой второй паре зажимов, вызывает на зажимах первой пары узлов то же самое напряжение.
Цепи, которые удовлетворяют теореме взаимности, называют взаимными или обратимыми.
Пример.
На рисунке 1.3а, показана схема цепи, для которой в чем легко убедиться, ток:
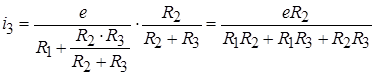 .
.
Требуется определить, чему будет равен ток ![]() (рис. 1.3б), если источник напряжения е перенести в ветвь с сопротивлением
(рис. 1.3б), если источник напряжения е перенести в ветвь с сопротивлением ![]() .
.
Ответ можно дать сразу же на основании теоремы взаимности:
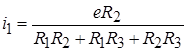 ,
,
а в правильности его следует убедиться, определив ![]() непосредственно из схемы (см. рис. 1.3б) традиционными методами.
непосредственно из схемы (см. рис. 1.3б) традиционными методами.
Применение резистивных цепей
В электрических цепях, составленных только из резисторов, реакция цепи ![]() (ток в любой ветви или напряжение между любыми узлами цепи) связана с воздействием
(ток в любой ветви или напряжение между любыми узлами цепи) связана с воздействием ![]() соотношением:
соотношением:
![]() ,
,
где А – не зависящий от времени коэффициент пропорциональности, откуда следует, что реакция резистивной цепи воспроизводит воздействие с точностью до постоянного множителя, т. е. колебания в резистивных цепях возникают в момент приложения воздействия, изменяются во времени по такому же закону, как и воздействия, и становятся равными нулю одновременно с равенством нулю воздействия.
Эти свойства резистивных цепей и определяют область их применения. В технике связи резистивные цепи применяются в качестве делителей напряжения, магазинов затуханий, измерительных мостов.