Реферат: Принцип Дирихле

Пример 16. В кубе с ребром a лежит ломаная, которую каждая плоскость, параллельная одной из граней, пересекает не более k раз. Доказать, что длина ломаной меньше 3ka.

Решение Введём в пространстве прямоугольную систему координат, оси которой направим вдоль рёбер куба. Пусть ломаная состоит из нескольких отрезков, длины которых мы обозначим через L_k .

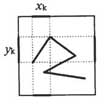Пусть x_k , y_k , z_k - проекции отрезка L_k на оси координат. Тогда L_k = [Ц(x² _k +y² _k +z² _k )]. Задачу будем решать методом от противного. Допустим, что длина ломаной не меньше 3ka. Тогда попробуем найти плоскость, параллельную одной из граней, которая пересечёт ломаную не менее чем в k+1 точках. Спроектируем ломаную на три грани куба, расположенные в плоскостях XOY, YOZ и XOZ, и рассмотрим одну из таких проекций, например, XOY (См. рисунок).

Каждый k-ый отрезок спроектированной ломаной образует также 4 проекции на сторонах квадрата, сумма длин которых равна 2(x_k + y_k ). Если сложить длины всех таких проекций для каждого отрезка, то получим S2(x_k + y_k ). Если бы эта величина была больше 4ka (т.е. более чем в k раз превосходила периметр квадрата), то по принципу Дирихле на одной из сторон квадрата нашлась бы точка, покрытая не менее чем k+1 проекциями. Тогда прямая, проведенная через эту точку и параллельная стороне квадрата, пересечёт проекцию исходной ломаной не менее чем в k + 1 точках. Значит, если через эту прямую провести плоскость, параллельную грани, то она пересечет исходную ломаную по крайней мере в k + 1 точках.

Осталось показать, что для одной из трёх граней, на которые проектировалась ломаная, сумма длин проекций, лежащих на сторонах квадрата, будет больше 4ka, т.е. одна из величин S2(x_k + y_k ), S2(z_k + y_k ), S2(x_k + z_k ) больше 4ka. Длина ломаной равна SL_k = S[Ц(x² _k +y² _k +z² _k )] и по предположению не меньше 3ka. Поэтому получаем

откуда

Если сумма трёх слагаемых больше 3·4ka, то по крайней мере одно из них больше 4ka, что и требовалось.

Непрерывный принцип Дирихле

Как правило, этот принцип применяется для нескольких чисел и их суммы. В общем виде для чисел он выглядит следующим образом:

"Если сумма n чисел больше S, то по крайней мере одно из этих чисел больше S/n".

По-другому его можно сформулировать так:

"Если среднее арифметическое нескольких чисел больше a, то хотя бы одно из этих чисел больше a";

или в терминах "зайцев":

"Если n кроликов съели m кг травы, то какой-то кролик съел не меньше m/n кг травы".

Кроме того, существует простая геометрическая интерпретация непрерывного принципа Дирихле:

"Пусть из некоторой точки на плоскости проведено N различных лучей; тогда угол между некоторыми двумя из них не менее 360^° /N".

Понятно, что если рассматривать только углы между соседними лучами, то всего получится N углов (См. рисунок). В сумме они составляют полный угол, равный 360^° . Следовательно,

по непрерывному принципу Дирихле градусная мера одного из этих углов не менее 360^° /N (иначе их сумма будет меньше 360^° ).

Рассмотренный принцип называется непрерывным постольку, поскольку здесь числа (или градусные меры углов) могут принимать любое значение из некоторого промежутка, в то время как принцип Дирихле в обычном смысле оперирует с дискретным набором объектов ("зайцев") - было бы абсурдным предполагать, что в клетке может оказаться, скажем, два с половиной зайца.

Пример 17. На плоскости дано n попарно непараллельных прямых. Доказать, что найдутся две из них, угол между которыми не меньше 180^° /n.

Указание. Достаточно перенести прямые параллельно самим себе так, чтобы все они проходили через одну точку. Из этой точки будет выходить 2n лучей, и теперь можно применить принцип Дирихле.

Пример 18. На полях шахматной доски 8×8 расставлены действительные числа, каждые два из которых отличаются не менее чем на 1/9. Доказать, что есть пара соседних (имеющих общую сторону) клеток, разность чисел в которых не меньше 1/2.

Решение Пусть A - наименьшее из выписанных на доске чисел, а B - наибольшее. Покажем, что B-A і7.

Запишем числа в порядке возрастания (заметим, что никакие два числа не равны):

(здесь x₁ = A, x₆₄ = B).

Тогда

Допустим теперь, что утверждение задачи неверно, т.е. в любой паре соседних клеток числа отличаются меньше чем на 1/2. Рассмотрим две клетки, в которых записаны числа A и B. Понятно, что, переходя из клетки в клетку, можно попасть из клетки A в клетку B, сделав не более 14 переходов. Самый худший случай, когда нужно сделать ровно 14 переходов, показан на рисунке (A, B - противоположные клетки). По предположению приращение на каждом переходе меньше 1/2. Поэтому B - A < 14·(1/2) = 7. Противоречие.

Список литературы

[1] Андреев А.А., Горелов Г.Н., Люлев А.И., Савин А.И. "Принцип Дирихле", Самара "Пифагор", 1997г